Moskva, Moscow, Russian Federation
A relevant didactic task is application in educational process on discipline «Higher mathematics» of technological diagnostics as modern control method of level of perception and assimilation of a training material. This work is carried out for the purpose of improvement of quality of mathematical training of future bachelor at the economic university. So far we accumulated experience of use of technological diagnostics in practice of teaching a subject matter «Higher mathematics», merits and demerits of technological approach to diagnostics of key and subject competences of future bachelor of management are specified. Practice of introduction and improvement of technological approach to teaching mathematical disciplines demonstrates that technological diagnostics allows to stir up educational cognitive activity of students of a bachelor degree, to quantitatively estimate and predict efficiency of activities for goal-setting and dispensing of a training material. The provisions presented in article and recommendations promotes increase in efficiency of educational process on mathematical disciplines, are of interest to teachers of mathematical disciplines at the higher economic school, can be used for modernization of already functioning methodical systems training to mathematical disciplines.
technological diagnostics; pedagogical design; pedagogical technology; educational process; the higher mathematics; mathematical preparation.
Совершенствование высшего экономического образования определяет ряд новых требований к методическим системам преподавания учебных дисциплин, включающих качественную и количественную диагностику прикладной математической подготовки бакалавров экономики, использование активных методов обучения [6, с. 126]. Одной из важных задач экономических университетов стала задача разработки, реализации и развития новых технологий обучения, обязательным компонентом которых является диагностика. Мы придерживаемся мнения о том, что необходим поэтапный переход от использования традиционных методов и приемов контроля знаний студентов к новым методам и приемам, раскрывающим потенциал информационных технологий.
Эмпирическим материалом для исследования возможностей технологической диагностики стали работы студентов факультета дистанционного обучения РЭУ им. Г.В. Плеханова. В процессе опытно-экспериментальной работы, которая охватывала ряд учебных дисциплин прикладной математической подготовки бакалавров, нами использованы как общенаучные, так и общепедагогические методы исследования. Отметим, что своевременная диагностика уровня усвоения учебного материала студентами бакалавриата является важным условием повышения эффективности учебного процесса.
Анализируя множество методов и приемов контроля знаний студентов, представленных в работах [9, 14, 17], мы пришли к выводу об особой роли технологической диагностики. Отметим, что правила организации и проведения системы технологических диагностик описаны в публикациях [11, 12, 13]. Практика создания и использования в учебном процессе технологических диагностик свидетельствует о возможности обеспечения устойчивой биективной связи между студентом и преподавателем. Технологическая диагностика выступает инструментом управления учебным процессом. Диагностика результатов по учебной дисциплине «Высшая математика» позволила нам своевременно определять реальный уровень овладения студентами бакалавриата умениями и навыками, выявлять имеющиеся проблемные зоны и выстраивать дальнейшую коррекционную работу. Технологическая диагностика результатов учебного-познавательной деятельности способствует более грамотному проектированию методических систем обучения на основе количественного анализа эффективности методов, приемов, средств и форм обучения.
Проектирование систем технологической диагностики и использование новых информационных технологий, некоторые из которых представлены в исследованиях [1, 2], в практике прикладной математической подготовки будущих бакалавров экономики свидетельствуют о направленности на развитие у студентов понятийного аппарата образовательной области «Математика», навыков решения прикладных математических задач, более эффективной организации самостоятельной работы в условиях сокращения аудиторной нагрузки.
Открытость и корректность технологических диагностик способствует развитию учебно-познавательной и научно-исследовательской деятельности студентов бакалавриата, в целом способствует повышению вариативности содержания подготовки бакалавров. Анализируя функции технологических диагностик, следует отметить, что они реализуют мотивирующую, обучающую, воспитательную и контролирующую функции.
Однако использование технологических диагностик в практике преподавания математических дисциплин имеет не только достоинства, но и недостатки. Среди достоинств применения технологических диагностик отметим следующие. Во-первых, объективность технологических диагностик. Все студенты погружены в одинаковую диагностическую среду, что способствует большей объективности оценивания знаний, умений и компетенций каждого студента и полностью исключает субъективизм оценивания. Осознание студентами правил прохождения технологических диагностик и понимание того, что эти правила не будут изменены преподавателем, способствует стимулированию их учебно-познавательной деятельности.
Во-вторых, оперативность технологических диагностик. Разработанный банк технологических диагностик по учебной дисциплине «Высшая математика» помогает оптимизировать использование учебного времени, а также личного времени преподавателя.
В-третьих, вариативность технологических диагностик. Содержание технологических диагностик подразумевает различные уровни сложности заданий, в том числе прикладные задачи социально-экономического содержания, позволяющие реализовывать межпредметные связи.
Четвёртой положительной чертой технологического диагностирования является массовость технологических диагностик – возможность охвата достаточно большого числа студентов благодаря применению современных информационных технологий. Как показывает практика внедрения в учебный процесс технологических диагностик, в них может принимать участие достаточно большое число студентов: как несколько групп студентов, так и весь поток студентов.
Так как каждая технологическая диагностика связана с соответствующим дозированием учебного материала, появляются более широкие возможности по актуализации самоконтроля. Используя блок технологического дозирования, студенты бакалавриата самостоятельно могут прорабатывать программный материал по учебной дисциплине «Высшая математика», самостоятельно анализируют степень усвоения теоретического материала, а также компетенции в области решения соответствующих задач. Результаты работы с технологическим блоком «Дозирование», связанным с последующей технологической диагностикой, способствуют прохождению студентом бакалавриата в случае необходимости дополнительного обучения по не полностью изученным учебным темам и типовым задачам.
Интеграция информационных и педагогических технологий [4, с. 110] в математической подготовке будущего бакалавра обеспечивает большее удобство в использовании технологических диагностик, способствует снижению трудоёмкости и практически исключает ошибки при проверке. Информационно-аналитические технологии [18] и профессиональные математические пакеты [3] позволяют в случае необходимости дистанционно оценивать знания, умения и компетенции студентов бакалавриата.
Однако использование технологического подхода к диагностике студентов в практике преподавания математических дисциплин имеет ряд недостатков. Во-первых, создание банка технологических диагностик требует существенных усилий со стороны преподавателя. Необходимо уделять внимание полноте диагностического материала, соответствию поставленным микроцелям по каждой учебной теме, исключающей случайное прохождение диагностики студентом. Отметим, что структура технологической диагностики предоставляет студенту право на ошибку, например по причине спешки или невнимательности. Как показывает практика внедрения педагогических технологий, это достаточно длительный и трудоемкий процесс.
Получаемые нами количественные оценки качества математической подготовки студентов бакалавриата в условиях внедрения педагогических технологий подтверждают принципиальную эффективность применения технологических диагностик в процессе преподавания математических дисциплин в экономическом университете. Технологический подход к диагностике результатов позволяет своевременно получить информацию о том, как проходит процесс восприятия и усвоения программного материала, совершенствования умений и компетенций, при необходимости корректировать блок «Целеполагание» [7, 8], а также более эффективно управлять учебно-познавательной деятельностью студентов в условиях информатизации образования.
Регулярное прохождение технологических диагностик способствует своевременное выявление и коррекция проблем и затруднений студентов, развитие самоконтроля и самообразования. Результат технологической диагностики – важный показатель, как для отдельного студента, так и для группы студентов. Результаты отражают не только соответствие содержания учебно-познавательной деятельности поставленной микроцели, но и динамику формирования качества подготовки студентов, что является мощным дидактическим инструментарием и стимулирует преподавателя высшей школы к выявлению и использованию новых дидактических закономерностей. Технология проектирования учебного курса [15, с. 42] предполагает использование входной, текущей и итоговой диагностик, охватывающих все уровни учебно-познавательной деятельности студентов бакалавриата. В содержательном плане диагностики сконструированы таким образом, что однозначно соответствуют поставленным микроцелям учебных тем.
Отметим, что большинство студентов испытывают определенные трудности в усвоении новых знаний по математическим дисциплинам. После обучения в школе многие первокурсники оказываются не в полной мере готовыми к эффективному усвоению программного материала, характеризующегося высоким уровнем абстракции, наличием формально-логических подходов к построению большинства понятий. Однако именно содержание учебных дисциплин, изучающихся на первом курсе, свяжется базисом для дальнейшего профессионального развития в условиях реализации идей контекстного обучения [10].
Так как ряд дисциплин математической подготовки преподаётся на первом курсе, то одной из задач применения технологических диагностик стало решение адаптационных проблем первокурсников, акцент на развитие механизмов самоконтроля и самооценки, не в полной мере развитых в процессе обучения в школе. Нами была поставлена задача создания банка технологических диагностик по учебным темам «Введение в математический анализ», «Дифференциальное исчисление», «Интегральное исчисление», «Дифференциальные уравнения», «Ряды», «Линейная алгебра», «Аналитическая геометрия», «Элементы теории чисел». Современное содержание образовательной области «Высшая математика» представлено в работах [19, 20]. Представим далее фрагмент банка технологических диагностик, внедренных на факультете дистанционного обучения РЭУ им. Г.В. Плеханова.
Диагностика 1. Вычислить пределы функций, не используя правило Лопиталя.
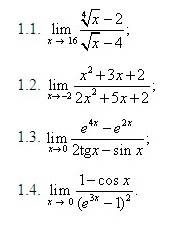
Диагностика 2. Вычислить пределы функций.
Диагностика 3. Найти производную заданных функций.
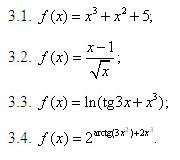
Диагностика 4. Найти производную заданных функций.
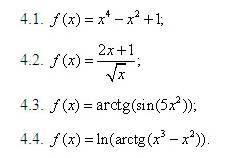
Диагностика 5. Определение интервалов монотонности и экстремумов заданной функции.
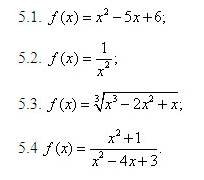
Диагностика 6. Определение направления выпуклости и точки перегиба графика заданной функции.
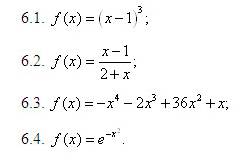
Проведенное исследование по технологизации учебного процесса в высшей экономической школе свидетельствует о том, что технологическая диагностика позволяет осуществлять своевременную коррекцию, способствует большей адаптации студентов к особенностям обучения в университете.
1. Aslanov R. M. Informacionnye tehnologii avtomatizirovannoy generacii zadaniy po differencial'nym uravneniyam [Tekst] / R. M. Aslanov, E. V. Belyaeva, S. A. Muhanov // Nauka i shkola. - 2015. - № 4. - S. 162-167.
2. Aslanov R.M. Trenazher po differencial'nym uravneniyam na osnove Wolfram CDF Player [Tekst] / R. M. Aslanov, E. V. Belyaeva, S. A. Muhanov // Sibirskiy pedagogicheskiy zhurnal. - 2015. - № 4. - S. 26-30.
3. Vlasov D.A. Vozmozhnosti professional'nyh matematicheskih paketov v sisteme prikladnoy matematicheskoy podgotovki buduschih specialistov [Tekst] / D. A. Vlasov // Vestnik Rossiyskogo universiteta druzhby narodov. Seriya: Informatizaciya obrazovaniya. - 2009. - № 4. - S. 52-59.
4. Vlasov D.A. Integraciya informacionnyh i pedagogicheskih tehnologiy v sisteme prikladnoy matematicheskoy podgotovki buduschego specialista [Tekst] / D. A. Vlasov // Sibirskiy pedagogicheskiy zhurnal. - 2009. - № 2. - S. 109-117.
5. Vlasov D.A. Kompetentnostnyy podhod k proektirovaniyu pedagogicheskih ob'ektov [Tekst] / D. A. Vlasov // Vestnik Federal'nogo gosudarstvennogo obrazovatel'nogo uchrezhdeniya vysshego professional'nogo obrazovaniya Moskovskiy gosudarstvennyy agroinzhenernyy universitet im. V.P. Goryachkina. - 2008. - № 6-2. - S. 124-127.
6. Vlasov D.A. Metody obucheniya kak komponent metodicheskoy sistemy prikladnoy matematicheskoy podgotovki [Tekst] / D. A. Vlasov // Yaroslavskiy pedagogicheskiy vestnik. - 2009. - № 4. - S. 125-129.
7. Vlasov D.A. Osobennosti celepolaganiya pri proektirovanii sistemy obucheniya prikladnoy matematike [Tekst] / D. A. Vlasov // Filosofiya obrazovaniya. - 2008. - № 4. - S. 278-283.
8. Vlasov D.A. Problemy proektirovaniya soderzhaniya prikladnoy matematicheskoy podgotovki buduschego specialista [Tekst] / D. A. Vlasov // Sibirskiy pedagogicheskiy zhurnal. - 2009. - № 8. - S. 33-42.
9. Kalinina E.S. Integrativnyy podhod k provedeniyu zanyatiy po matematicheskim disciplinam v Vuzah MChS Rossii [Tekst] / E. S. Kalinina // Nauchno-analiticheskiy zhurnal Vestnik Sankt-Peterburgskogo universiteta Gosudarstvennoy protivopozharnoy sluzhby MChS Rossii. - 2017. - № 2. - S. 187-193.
10. Kalinina E.S. O kontekstnom podhode v obuchenii matematicheskim disciplinam v Vuzah MChS Rossii [Tekst] / E. S. Kalinina // Sovremennoe obrazovanie: soderzhanie, tehnologii, kachestvo. - 2017. - № 1-9. - S. 59.
11. Monahov V.M. Vvedenie v teoriyu pedagogicheskih tehnologiy monografiya [Tekst] / V. M. Monahov; M-vo nauki i obrazovaniya RF, Feder. agentstvo po obrazovaniyu, Mezhvuz. centr distanc. obrazovaniya MGOPU im. M. A. Sholohova, Volgograd. gos. ped. un-t. Volgograd, 2006. - 241 s.
12. Monahov V.M. Diagnostika [Tekst] / V. M. Monahov - Moskva-Novokuzneck: Novokuzneckiy IPK, 1997. - 75s.
13. Monahov V.M. Pedagogicheskie ob'ekty. Pedagogicheskoe proektirovanie. Know How tehnologii uchebnoe posobie [Tekst] V. M. Monahov, A. N. Yarygin, A. A. Korostelev - Tol'yatti, 2004. - 65 c.
14. Muhanov S.A. Ispol'zovanie informacionnyh tehnologiy dlya individualizacii obucheniya matematike na primere temy «Differencial'nye uravneniya» [Tekst] / S. A. Muhanov, A. A. Muhanova, A. I. Nizhnikov // Vestnik Moskovskogo gorodskogo pedagogicheskogo universiteta. Seriya: Informatika i informatizaciya obrazovaniya. - 2018. - № 1 (43). - S. 72-77.
15. Muhanov S.A. Proektirovanie uchebnogo kursa [Tekst] / S. A. Muhanov, A. I. Nizhnikov // Pedagogicheskaya informatika. - 2014. - № 4. - S. 39-46.
16. Pantina I.V. Vychislitel'naya matematika [Tekst] / I. V. Pantina, A. V. Sinchukov - M.: MFPU «Sinergiya», 2012. - 176 s.
17. Sinchukov A.V. Didakticheskiy potencial Wolframalpha v prepodavanii matematicheskih disciplin v ekonomicheskom universitete [Tekst] / A. V. Sinchukov // Vestnik gumanitarnogo obrazovaniya. - 2017. - № 4. - S. 23-27.
18. Smirnov E.I. Proektirovanie informacionno-analiticheskih tehnologiy obucheniya studentov-ekonomistov [Tekst] / E. I. Smirnov, E. N. Trofimec // Yaroslavskiy pedagogicheskiy vestnik. - 2010. - T. 2. - № 2. - S. 137.
19. Suhorukova I.V. Komp'yuternoe modelirovanie i matematicheskoe obespechenie ekonomiko-social'nyh zadach [Tekst] / I. V. Suhorukova, G. G. Lihachev // Ekonomicheskiy analiz: teoriya i praktika. - 2003. - № 5. - S. 60-62.
20. Tatarnikov O.V. Matematika dlya ekonomistov [Tekst] / O. V. Tatarnikov, R. V. Sagitov, A. S. Chuyko, E. V. Shved, V. G. Shershnev - M.: Izdatel'stvo Yurayt, 2015. - 593 s.
