сотрудник
Россия
сотрудник
г. Москва и Московская область, Россия
Предложена концепция формирования спецкурса по экономическим приложениям Марковских процессов для студентов экономических ВУЗов. Даны методические рекомендации преподавания такой дисциплины, знакомящей слушателей с прикладными аспектами математической теории Марковских процессов. На основе многолетнего обобщенного опыта преподавания дисциплины в РЭУ описана структура построения курса, его взаимосвязь с другими дисциплинами. сформулированы цели и задачи дисциплины. Приведено подробное описание рассматриваемых тем и предложены конкретные примеры характерных задач, имеющих как теоретическую так и вычислительную направленность. Предложен алгоритм выполнения и контроля самостоятельной работы студентов. Приведены образцы индивидуальных расчетно-аналитических работ. Сформулированы критерии оценки знаний слушателей, приведен список теоретических вопросов итоговой аттестации . Практическая направленность иллюстрирующих примеров даже при серьезных теоретических основах позволяет заинтересовать студентов широкого круга направлений обучения. Разработанный подход позволяет расширить профессиональные и общекультурные компетенции студентов, направленные на применение математических методов анализа в экономических приложениях, а также формирует научное мировоззрение и помогает устанавливать причинно-следственные связи в прикладных исследованиях. Практика преподавания дисциплины в РЭУ в виде дисциплины по выбору показала ее востребованность студентами и стабильно демонстрирует интерес к задачам этого направления. Компьютерная поддержка обучения существенно дополняет методы самостоятельной работы студентов, разнообразит ее, развивает навыки современной работы с данными, экономит время и вносит заинтересованность в быстрое получение результата.
Марковский процесс, цепь Маркова, оптимальное управление, методика преподавания, расчетные задания
В новом государственном стандарте (ФГОС) повышенное внимание уделяется обучению студентов навыкам анализа прикладных постановок задач. Стандарт требует сформировать у выпускников профессиональные компетенции, направленные на грамотное использование полученных знаний при решении возникающих практических задач. Это вызвало необходимость интенсивного использование математических моделей в экономических исследованиях и более детального их изучения [1-4 ]. Одной из прикладных моделей для исследования постановок задач в экономических и технических областях является модель Марковского процесса, знакомство с которым в экономическом ВУЗе обычно либо вообще отсутствует, либо происходит весьма поверхностно в курсе теории вероятностей. Поэтому целесообразно на старших курсах вернуться в виде дисциплины по выбору студентов или спецкурса в рамках вариативной части учебного плана к более глубокому обучению студентов методам анализа Марковских процессов и познакомить их с разными постановками практических задач с использованием модели таких процессов [5-10 ]. Наполнение дисциплины существенно зависит от математической подготовки слушателей и выделенного времени на ее изучение, поэтому количество тем и учебных материалов может сильно варьироваться для студентов с разными уровнями подготовки. Мы предлагаем концепцию формирования спецкурса по приложениям Марковских процессов на основе опыта преподавания дисциплины «Экономические приложения Марковских процессов» для студентов направлений «Прикладная математика и информатика», «Математические методы в экономике» и «Менеджмент» в РЭУ им. Г.В.Плеханова. В отличие от продвинутого курса Марковских процессов, читаемых для естественнонаучных специальностей университетов, здесь существенно сокращены доказательства рабочих теорем и предлагаются готовые алгоритмы решения практических задач, базирующиеся на этих теоремах. Такой подход позволяет расширить профессиональные и общекультурные компетенции студентов, направленные на применение математических методов анализа в экономических приложениях, а также формирует научное мировоззрение и помогает устанавливать причинно-следственные связи в прикладных исследованиях. Практика преподавания дисциплины в РЭУ в виде дисциплины по выбору показала ее востребованность студентами и стабильно демонстрирует интерес к задачам этого направления. Компьютерная поддержка обучения существенно дополняет методы самостоятельной работы студентов, разнообразит ее, развивает навыки современной работы с данными, экономит время и вносит заинтересованность в быстрое получение результата.
В данной работе мы хотим остановиться на методах преподавания дисциплины «Экономические приложения Марковских процессов» в РЭУ им. Г.В.Плеханова и предложить концепцию учебной рабочей программы этой дисциплины. Целями дисциплины являются изучение математических методов анализа дискретных и непрерывных цепей Маркова, а также изучение методов управления экономическими Марковскими процессами. Задачами дисциплины являются:
1. построение формальных моделей социально-экономических процессов в терминах дискретных и непрерывных цепей Маркова;
2. анализ структуры моделирующего процесса;
3. расчет характеристик процесса;
4. поиск оптимального управления Марковским процессом с доходами, максимизирующими полный ожидаемый доход, предельный доход или прибыль.
Для успешного освоения дисциплины необходимо предшествующее изучение следующих дисциплин: «Линейная алгебра», «Математический анализ», «Дифференциальные уравнения», «Теория вероятностей и математическая статистика». Студент должен знать основные определения и свойства алгебраических объектов, методы математического анализа и теории вероятностей, владеть техникой работы с векторными и матричными данными на компьютере, техникой решения дифференциальных уравнений, вычисления вероятностей событий и анализом поведения случайных величин и случайных векторов.
Тематический план изучения дисциплины рассчитан на 56 часов аудиторной работы, 52 часа самостоятельной работы и включает следующие темы: тема 1 – дискретные цепи Маркова, тема 2 – управление дискретными цепями Маркова с доходами, тема 3 – непрерывные цепи Маркова и связанные с ними прикладные задачи. Содержание тем дисциплины «Экономические приложения Марковских процессов» приведено ниже.
|
ТЕМА 1. Дискретные цепи Маркова |
Основные определения. Уравнения Колмогорова-Чепмена. Матрица вероятностей переходов за n шагов. Вектор вероятностей состояний системы через n шагов. Анализ структуры цепи Маркова: существенные и несущественные состояния, разложимость и неразложимость цепи, структура класса эквивалентности (регулярная и циклическая), построение циклических подклассов класса эквивалентности, каноническая нумерация состояний и построение матрицы вероятностей переходов в канонической форме. Классификация дискретных цепей Маркова. Стационарный и неподвижный векторы вероятностей состояний. Эргодические теоремы долгосрочного прогноза поведения неприводимой, моноэргодической, полиэргодической поглощающей цепи и полиэргодической цепи общего вида. Пример задачи о разорении игрока в игре двух лиц (вычисление вероятности разорения каждого из игроков при фиксированных начальных ставках и вероятностях выигрыша одной ставки, вычисление средней продолжительности игры и среднего выигрыша игрока). Пример модели Морана в теории запасов. |
|
ТЕМА 2. Управление дискретными цепями Маркова с доходами
|
Понятие дискретной цепи Маркова с доходами. Матрица одношаговых доходов. Векторы среднего одношагового дохода и полного ожидаемого дохода системы за n шагов. Матричное уравнение для полного ожидаемого дохода системы за n шагов с учетом и без учета процентной ставки и его компьютерное решение. Асимптотика полного ожидаемого дохода системы. Понятия стратегии, политики и управления для цепи Маркова. Построение оптимального управления, максимизирующего полный ожидаемый доход системы при конечном горизонте управления методом динамического программирования Беллмана. Построение методом Ховарда оптимального управления, максимизирующего предельный доход или прибыль в классе стационарных управлений при бесконечном горизонте управления. |
|
ТЕМА 3. Непрерывные цепи Маркова и связанные с ними прикладные задачи..
|
Простейший поток событий и пуассоновский процесс, его свойства. Дифференциально-разностные уравнения Колмогорова для вероятностей состояний непрерывной цепи в произвольный момент времени и их решение с помощью преобразования Лапласа, стационарные вероятности состояний. Процессы гибели и размножения с непрерывным временем, их частные случаи. Дифференциальные уравнения для вероятностей состояний в произвольный момент времени и их решение, стационарный режим. Прикладные задачи анализа процессов и систем обслуживания с помощью непрерывных цепей Маркова |
По теме 1 предлагается решить задачи, имеющие как теоретический, так и вычислительный характер.
Задача 1. В вычислительном центре три компьютера. Каждый в течение дня может сломаться с вероятностью q=0.3 и встать на ремонт. Вероятность починки в течение дня равна r=0.2. За один день и сломаться, и починиться компьютер не может. Состояние системы в момент n – количество исправных компьютеров в этот момент. Опишите функционирование системы в виде цепи Маркова, дайте полный структурный анализ цепи. Найдите матрицу переходных вероятностей и вектор вероятностей состояний цепи через неделю работы, если в начальный момент все компьютеры исправны.
Задача 2. В процессе ежемесячного погашения выданного кредита клиент банка может оказаться в одном из следующих состояний
i=1 - ежемесячный платеж погашен в срок в полном объеме,
i=2 - ежемесячный платеж погашен в полном объеме, но с временной задержкой,
i=3 - ежемесячный платеж погашен в срок в неполном объеме с переходом остатка долга на следующий месяц,
i=4 - ежемесячный платеж погашен с временной задержкой и в неполном объеме с переходом остатка долга на следующий месяц.
Последовательные состояния образуют цепь Маркова с матрицей вероятностей перехода вида
Дайте полный структурный анализ цепи. Найти вероятности состояний после трех месяцев, если первый платеж был в срок.
Задача 3. Допустим, что в некотором городе каждый год 4% жителей переселяются в пригороды, а 1% жителей пригородов переселяются в город. Предполагая, что общее число жителей остается постоянным, опишите процесс перераспределения населения в виде цепи Маркова, дайте полный структурный анализ цепи. Найдите матрицу переходных вероятностей, найдите финальное распределение жителей между городом и пригородом.
По теме 1 в рабочей программе дисциплины предусмотрена индивидуальная расчетно-аналитическая работа, состоящая из анализа трех дискретных цепей Маркова возрастающей сложности: первая – неприводимая, или моноэргодическая цепь, вторая – полиэргодическая поглощающая цепь, третья – полиэргодическая цепь общего вида. Приведем один вариант графов цепей Маркова для расчетно-аналитической работы.
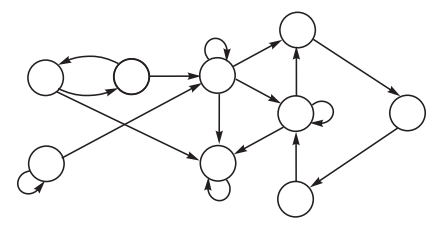
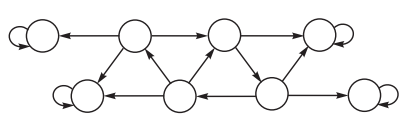
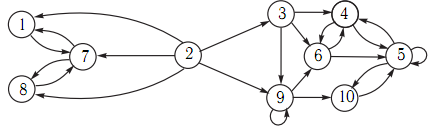
Получив свои индивидуальные графы цепей Маркова, студент сначала выполняет письменное домашнее задание по проведению структурного анализа цепей и сдает его на проверку. Сюда включены следующие задачи:
- дать полный структурный анализ цепи Маркова, введя каноническую нумерацию состояний, определить тип цепи;
- задать вероятности переходов, отметив их на графе состояний;
- найти матрицу переходов в канонической форме.
После проверки заданий и исправления ошибок выполняется вторая часть расчетного задания на занятии в компьютерном классе. Сюда включены следующие задачи:
- задать равновероятный вектор начальных вероятностей состояний цепи и найти вектор вероятностей состояний цепи через три шага;
- пользуясь соответствующей эргодической теоремой, найти финальную матрицу вероятностей переходов цепи и стационарный вектор вероятностей состояний. Дать смысловую интерпретацию разных фрагментов финальной матрицы вероятностей переходов.
В теме 2 рассматриваются теория и задачи на получение полного ожидаемого дохода и поиск оптимального управления Марковской цепью с доходами. Приведем несколько примеров
Задача 4. При сдаче сессии на отлично назначается повышенная стипендия, при сдаче на 4 и 5 - обычная стипендия. Состояние студента =1,2,3, если у него повышенная стипендия, обычная стипендия, или нет стипендии соответственно. Матрицы вероятностей переходов и одношаговых доходов имеют вид P и R и приведены ниже. Найдите полный ожидаемый доход за 4 года обучения случайно выбранного студента, если дисконтный множитель за семестр равен 0.95. Чему равна величина полного ожидаемого дохода, если студент начинал учиться без стипендии? Какой средний объем стипендиального фонда расходуется на всех студентов, если в первом семестре всем платят обычную стипендию, а в ВУЗе 2000 студентов?
|
0,3 |
0,6 |
0,1 |
|
16080 |
8040 |
0 |
||
|
Р= |
0,2 |
0,5 |
0,3 |
|
R= |
16080 |
8040 |
0 |
|
матрица |
0,05 |
0,25 |
0,7 |
|
матрица |
16080 |
8040 |
0 |
|
переходов |
|
доходов |
||||||
|
за семестр |
|
за семестр |
Задача 5. Ежегодно можно выбрать государственную, либо частную управляющую компанию для хранения своих пенсионных накоплений (состояние 1 и 2 соответственно). Состояние системы –выбранный тип компании. Матрицы вероятностей переходов и одношаговых доходов имеют вид Р и R и приведены ниже. Найдите предельный полный ожидаемый доход, если процентная ставка равна 7%.
|
Р= |
0,9 |
0,1 |
|
R= |
40000 |
50000 |
|
матрица |
0,8 |
0,2 |
|
матрица |
40000 |
30000 |
|
переходов |
|
доходов за год |
Построение оптимального управления экономической системой, имеющей вид цепи Маркова, проиллюстрируем с помощью последовательных задач руководителя фирмы.
Задача 6. Деятельность фирмы в течение месяца имеет два состояния: сбыт высокий (состояние 1) и сбыт низкий (состояние 2). Ее матрица вероятностей переходов имеет вид Р=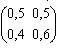
, матрица одношаговых доходов равна R=
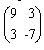. Найдите полный ожидаемый доход фирмы за год, если процентная ставка равна 6%.
Задача 7. Продолжая рассмотрение задачи руководителя фирмы, найдите предельный доход, если процентная ставка равна 6%.
Задача 8. Продолжим рассмотрение задачи руководителя фирмы с двумя состояниями: i=1 - объем сбыта высокий и 1=2 - объем сбыта низкий. В каждом состоянии и на каждом шаге можно воспользоваться одной из двух стратегий:
а) ki= 1 - не использовать рекламу. При этом матрица вероятностей переходов имеет вид Р=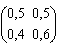
, матрица одношаговых доходов равна R=
;
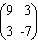б) ki= 2 - руководитель фирмы организует рекламную кампанию, это позволяет увеличить вероятности перехода в первое состояние ценой снижения ожидаемых доходов текущего месяца, а именно, матрица вероятностей переходов имеет вид Р=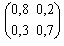
, матрица одношаговых доходов равна R=
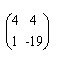. Найдите четыре значения вектора предельных доходов для четырех вариантов управления.
Задача 9. Продолжим рассмотрение задачи руководителя фирмы. Методом динамического программирования Беллмана найдите оптимальное управление и соответствующее ему значение полного ожидаемого дохода, если горизонт управления равен 5 месяцам, а влияние процентной ставки не учитывается.
Перейдем к теме 3, в которой, как указано выше, исследуются марковские цепи с непрерывным временем и связанные с ними прикладные задачи. Приведем примеры задач на эту тему.
Задача 10. Покупатели образуют простейший поток интенсивности 3. Вероятность того, что покупатель совершит покупку, равна 0.9. Найдите средний интервал между покупателями, ушедшими без покупки.
Задача 11. Дан граф состояний, описывающий работу системы.
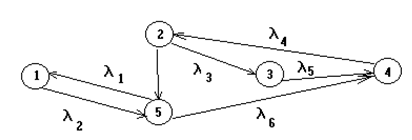
Задав на графе состояний интенсивности переходов, напишите уравнения Колмогорова для вероятностей состояний в произвольный момент времени и эквивалентную систему уравнений для преобразований Лапласа. Найдите стационарные вероятности
Задача 12. В систему с двумя обслуживающими приборами без мест для ожидания поступает простейший поток требований интенсивности 1 и поступает на обслуживание по следующему правилу. Требование обслуживается первым прибором, если он свободен, вторым прибором, если первый занят, но второй свободен, требование теряется, если на момент его поступления оба прибора заняты. Приборы имеют разную производительность. Среднее время обслуживания на первом приборе 0.5, на втором приборе 0.25. Нарисуйте граф интенсивностей переходов, указав, что является состоянием системы. Найдите вероятность того, что система пуста и что полностью загружена (в стационарном режиме). Придумайте содержательную интерпретацию этой задачи.
Задача 13. Аудиторская компания последовательно проверяет четыре предприятия. Время проверки имеет экспоненциальный закон распределения и в среднем равно полумесяцу. Предприятия однотипны и независимы. Из прошлого опыта проверок можно утверждать, что с вероятностью 0.4 будут обнаружены нарушения в работе предприятия. Введем два случайных процесса – число проверенных предприятий в момент t и число проверенных предприятий в момент t, у которых обнаружены нарушения в работе. Найдите законы распределения этих характеристик, а при t=2 дайте числовой ответ.
Задача 14. (продолжение) Аудиторы разделились на четыре равные группы, каждая группа начинает проверку своего предприятия. Найдите закон распределения числа проверенных предприятий в момент t.
Текущий контроль по дисциплине состоит в аттестации расчетно-аналитической работы по теме 1, о которой речь шла выше. В случае успешного выполнения работы задачи по этой теме не выносятся на итоговую аттестацию, но, естественно, учитываются в общем рейтинге студента по дисциплине. Итоговый контроль в виде зачета или экзамена предусматривает аттестацию только по темам 2 и 3 и состоит из теоретических вопросов и задач. В случае задолженности по теме 1 итоговая аттестация включает материал по всем темам. Приведем примерный список теоретических вопросов.
- Марковский процесс с конечным пространством состояний и дискретным временем. Граф состояний и матрица вероятностей перехода цепи Маркова.
- Уравнения Колмогорова-Чепмена. Матрица вероятностей перехода цепи Маркова за n шагов. Вычисление вероятностей состояний цепи Маркова через n шагов.
- Анализ структуры пространства состояний цепи. Основная теорема структурного анализа и ее следствия. Каноническая нумерация состояний цепи.
- Регулярные и циклические классы эквивалентности существенных состояний цепи. Исследование класса эквивалентности на цикличность.
- Классификация дискретных цепей Маркова. Полный структурный анализ цепи. Вид матрицы вероятностей перехода цепи при канонической нумерации ее состояний Пример.
- Долгосрочный прогноз эволюции цепи. Сильная и слабая сходимость матрицы вероятностей перехода и вектора вероятностей состояний за n шагов к финальной матрице вероятностей перехода и финальному вектору вероятностей состояний.
- Эргодическая теорема о предельном поведении неразложимой цепи.
- Долгосрочный прогноз эволюции моноэргодической цепи..
- Долгосрочный прогноз эволюции полиэргодической поглощающей цепи. Поиск предельных вероятностей разорения и выигрыша а также среднего предельного выигрыша в задаче о разорении.
- Долгосрочный прогноз эволюции полиэргодических цепей общего вида. Алгоритмы поиска финальной матрицы вероятностей перехода и финального вектора вероятностей состояний.
- Дискретные цепи Маркова с доходами. Вычисление полного ожидаемого дохода.
- Предельное поведение полного ожидаемого дохода.
- Марковский процесс с конечным пространством состояний и непрерывным временем. Граф состояний.
- Простейший поток событий. Слияние и просеивание простейших потоков.
- Дифференциальные уравнения Колмогорова для вероятностей состояний цепей Маркова с непрерывным временем
- Решение уравнений Колмогорова для вероятностей состояний цепей Маркова с использованием преобразования Лапласа.
- Финальные вероятности состояний цепей Маркова с непрерывным временем.
- Процесс чистого размножения. Вычисление вероятностей состояний.
- Процесс чистой гибели. Вычисление вероятностей состояний.
- Стационарный режим процесса гибели и размножения. Финальные вероятности состояний.
- Системы массового обслуживания как приложения Марковских процессов с непрерывным временем
В заключение отметим, что дисциплина допускает большую вариативность изложения, как по глубине, так и по объему материала. Практическая направленность иллюстрирующих примеров даже при серьезных теоретических основах позволяет заинтересовать студентов широкого круга направлений обучения. Кроме того такая дисциплина полезна в форме дополнительного образования и для технических направлений обучения, и для экономических. Получаемые знания и навыки найдут применение в практических постановках задач, в умении системно их решать с помощью универсальных разработанных методов, в принятии управленческих решений. Надеемся, что рекомендации и подборка задач будут полезны не только студентам, но и всем, кого интересуют Марковские процессы и управление ими.
1. Sukhorukova I.V., Chistyakova N.A., Methodical Aspects of Actuarial Mathematics Teaching . //Astra Salvensis .2018. Vol.VI , Special Issue, pp. 847-857.
2. Popov V.A., Inflation and consumer basket // Journal of Reviews on Global Economics. , 2018, vol . 7, No. Special Issue , pp. 453-456.
3. Sukhorukova I.V, Chistyakova N.A., (2018), Economic regulation and mathematical modeling of insurance product cost, // Journal Regional Science Inquiry, Vol. X (2), pp. 195-203
4. Киселев В.Ю., Калугина Т.Ф. Процесс параллельной эксплуатации в учебном курсе марковских процессов и теории массового обслуживания . В сборнике: Инженерные и социальные системы Сборник научных трудов инженерно-строительного института ИВГПУ. 2017. С. 58-61.
5. Casas J.M., Ladra M., Rozikov U.A. Markov processes of cubic stochastic matrices: quadratic stochastic processes ”, // Linear Algebra and its Applications, 2019 vol. 575, pp. 273-298.
6. Sukhorukova I.V, Chistyakova N.A., (2019) Insurance of the termination risk of projects with joint companion activity., // Journal of Reviews on Global Economics. vol. 8, pp. 269-274.
7. Antoniou I., Bosco F. On the spectral properties of a Markov model for learning processes, International //Journal of Modern Physics , 2000. vol. 11., No 2, pp. 213-220.
8. Muhly P.S., Solel B. Quantum Markov processes (correspondences and dilations) , //International Journal of Mathematics,, 2002 . vol. 13, № 8, pp. 863-906.
9. Власов Д.А., Синчуков А.В. MS EXCEL как система поддержки принятия решений // International Journal of Open Information Technologies, 2019, Т. 7, № 3, С. 50-59
10. Frank T.D. A note on the Markov property of stochastic processes described by nonlinear Fokker-Planck equations, //Physica A: Statistical Mechanics and its Applications., 2003 vol. 320, pp. 204-210.
