Tula, Russian Federation
Finding the largest and smallest values of a function, an optimization problem, is not only of practical importance, but also of great importance for the development of students' thinking. The pupil develops the most important skill in the formulation of such tasks, their analysis and methods of solution. The article deals with the question of how this very important topic is revealed in school textbooks. We are mainly considering not only the existing textbooks on algebra and analysis, but also geometry. A comparative analysis of these textbooks is carried out so that the teacher could choose the most suitable one from his own understanding. For the convenience of the reader, almost all the problems formulated in the textbooks are given in the article. In addition to school textbooks, the reader is recommended books [1] and [2], in which the topic under discussion is presented in the most general form.
maximum, minimum, unconditional and conditional extremes, optimization problem, objective function, set of admissible solutions, stationary and critical points, Weierstrass theorem.
В школе изучают функции только одной переменной, заданные на числовой прямой R, поэтому применительно к этому под оптимизационными (или экстремальными) задачами понимают те, в которых задана некоторая функция 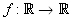 , которую называют целевой функцией, «ее значения характеризуют степень достижения цели, во имя которой поставлена или решается задача» [1, с. 6], и некоторое подмножество
, которую называют целевой функцией, «ее значения характеризуют степень достижения цели, во имя которой поставлена или решается задача» [1, с. 6], и некоторое подмножество 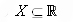 (называемое множеством допустимых решений), «среди элементов которого осуществляется поиск». Требуется найти точку
(называемое множеством допустимых решений), «среди элементов которого осуществляется поиск». Требуется найти точку  , в которой достигается наибольшее или наименьшее значения, или установить, что таких точек нет.
, в которой достигается наибольшее или наименьшее значения, или установить, что таких точек нет.
Если при этом 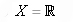 , то ищется безусловный экстремум, а если и задается с помощью равенств и (или) неравенств, то ищется условный экстремум. Сокращенно это записывается так:
, то ищется безусловный экстремум, а если и задается с помощью равенств и (или) неравенств, то ищется условный экстремум. Сокращенно это записывается так:

В школьном курсе Х может быть прямой, лучом, отрезком, полуоткрытым отрезком или открытым отрезком.
Оптимизационные задачи в школьных учебниках алгебры и анализа 10-11 классов
Учебник под редакцией А. Н. Колмогорова
Данный учебник [3] написан не только под руководством великого математика, но и человека, который увлеченно преподавал долгое время в школе. Оптимизационные задачи разбираются в разделе, специально для этого написанного: «Наибольшее и наименьшее значение функции». После необходимых определений дается очень полезная для общего развития теорема Вейерштрасса, с помощью которой обосновывается следующее правило поиска экстремальных значений:

Этот алгоритм шаг за шагом реализуется на примере решения двух задач. Цель, с которой в учебнике рассматривается эта тема, сформулирована так [3, с. 156]:

Для решения оптимизационных задач в учебнике приводится очень полезная схема (алгоритм):

Затем идет серия хорошо подобранных задач из алгебры, геометрии, физики. Вопросы оптимизации со всех сторон обсуждаются в хорошем историческом обзоре. Даже после такого подробного изучения оптимизационных задач о них речь идет и при изучении последующих тем. Например, в теме «Интеграл» рассматриваются задачи на нахождение наименьшего и наибольшего значений определенных интегралов.
Учебник Мордковича А. Г.
Тема оптимизации начинается в учебнике [4] в специально написанном разделе «Применение производной для нахождения наибольших и наименьших значений величин» на с. 192. Теорема Вейерштрасса, как и в учебнике [3], тоже формулируется, но почему-то без указания фамилии Вейерштрасса. В отличие от учебника [3], при формулировке алгоритма нахождения экстремальных значений различают понятия стационарной и критической точек, которые в [3] относятся к критическим.

Далее на нескольких примерах показывается, как решать задачи, применяя этот алгоритм по шагам.
Специально рассматривается тема оптимизации на незамкнутых отрезках для случая единственной стационарной или критической точки с разбором задач.
Так же, как и в книге [3], рассматривается цель, с которой изучаются задачи оптимизации: а именно, моделирование практических задач, но более подробно, с формулировкой алгоритма составления и изучения модели с пошаговым разбором нескольких примеров.
При изучении последующих тем время от времени решаются и задачи на оптимизацию.
Очень полезна тема функционально-графического метода решения уравнений с применением методов оптимизации (с. 358):

В целом, учебник [4] производит впечатление очень подробного и многословного пересказа учебника [3], что, возможно, полезно тем учителям, которым кратко и изящно написанный текст [3] требуется дополнительно разъяснить.
Учебник Алимова Ш. А. и др.
В книге [5] производная рассматривается только после предварительного введения и изучения элементарных функций, тема оптимизации рассматривается в главе IX, §52 «Наибольшее и наименьшее значения функции».
Теорема Вейерштрасса вообще не формулируется, а сразу дается «рецепт» нахождения наибольшего и наименьшего значений функции без всякого обоснования:
Для нахождения наибольшего или наименьшего значения функции на отрезке [a; b] нужно:
1) найти значения функции на концах отрезка, т.е. числа f(a) и f(b);
2) найти ее значения в тех критических точках, которые принадлежат интервалу (a; b);
3) из найденных значений выбрать наибольшее и наименьшее.
Затем пошагово разбираются 4 задачи для двух функций, из теории чисел и из геометрии. Мотивировок, формулировки цели нет. Далее в теме «Интеграл» оптимизационные задачи не появляются вовсе. В этом смысле книга существенно уступает книгам [3] и [4].
Более сложные задачи оптимизации имеются в конце учебника для внеклассного решения.
Оптимизационные задачи в школьных учебниках геометрии 9-х, 10-х и 11-х классов
Учебник под редакцией Атанасяна Л. С.
В книге [6] оптимизационные задачи как таковые не вводятся.
В главе 4 среди задач на построение приведена классическая задача, которую должен знать любой школьник:

Эта задача еще раз дублируется под номером 1175.
Среди дополнительных задач к теме «Окружность» приведена задача:
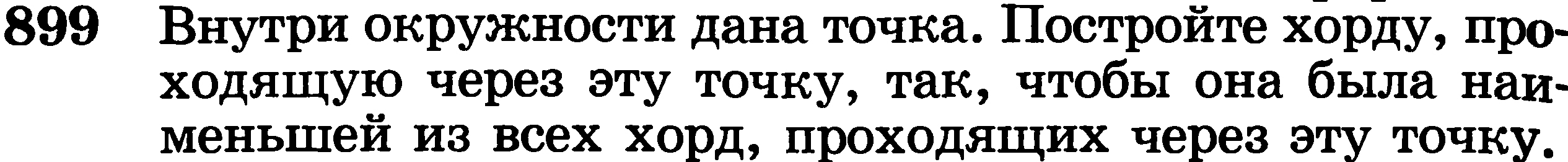
К этой задаче имеется указание: Сначала доказать, что наименьшей будет хорда перпендикулярная к диаметру, проходящему через данную точку.


В конце учебника среди задач повышенной сложности имеется такая:

Задача относится к темам: «развертка куба» и «кратчайшая линия на плоскости».
На наибольшее значение никаких стоящих задач вообще нет, если не считать «псевдозадачу» 1091…
Таким образом, в курсе 9-го класса в указанном учебнике вообще не обсуждаются оптимизационные задачи, вышеуказанные задачи приведены без всякой мотивации.
В учебнике геометрии [7] для 10–11 классов тема оптимизации вообще никак не отражена.
Учебник Киселева А.П.
Как мы видели, в учебнике геометрии под ред. Атанасяна задача оптимизации как таковая вообще не ставится, то же самое можно утверждать и о старых учебниках геометрии, популярных в прошлом. Есть просто некоторый набор задач на эту тему. В учебнике А.П. Киселева [10] практически все оптимизационные задачи появляются как задачи на построение.
стр. 53 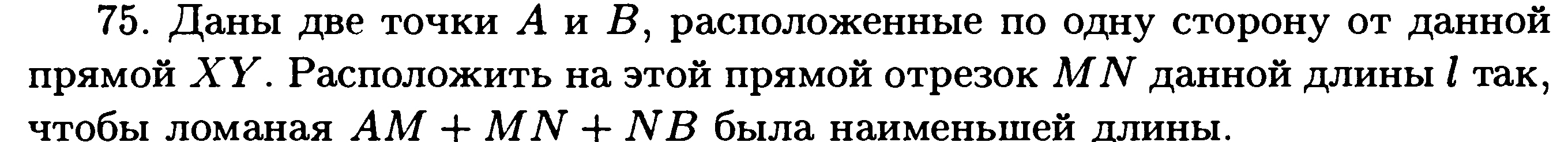
стр. 73 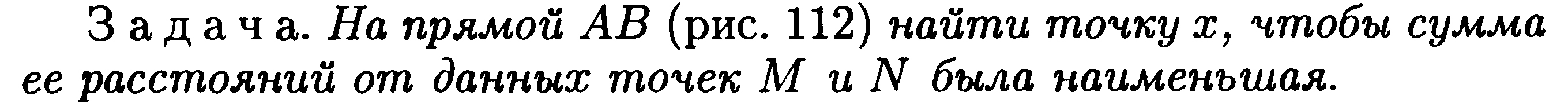
стр. 78
стр. 98
стр. 240
1. [9, задача 5.11(3)]. Сумма n положительных чисел равна a. Докажите, что произведение этих чисел максимально, если каждое из них равно a/n.
Доказательство.
Известно неравенство Коши о среднем арифметическом и среднем геометрическом для неотрицательных чисел:
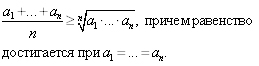
По условию 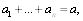 a при достижении равенства правая часть, то есть произведение чисел, достигает максимума.
a при достижении равенства правая часть, то есть произведение чисел, достигает максимума.
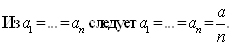
2. [9, задача 5.11(18)]. Дождевая капля, начальная масса которой равна m граммов, а начальная скорость равна нулю, падает под действием силы тяжести, равномерно испаряясь так, что масса уменьшается пропорционально времени (коэффициент пропорциональности равен k г/с). Через сколько секунд после начала падения кинетическая энергия капли будет наибольшей?
Решение
В момент времени t масса капли равна m – kt, скорость равна vt, тогда кинетическая энергия равна
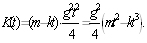
Ставим задачу
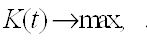
Приравняв производную от K нулю, получаем
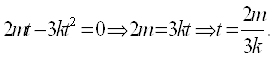
Производная меняет знак при переходе через эту точку с + на -, здесь точка максимума. Так как на луче (0; +∞) она единственная, то в этой точке достигается не только максимум, но и наибольшее значение, которая равна 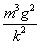 дина.
дина.
3. [9, задача 5.11(19)]. Из пункта А, находящегося в лесу в 5 км от прямолинейной дороги, пешеходу нужно попасть в пункт В, расположенный на этой дороге в 13 км от пункта А. По дороге пешеход может двигаться с максимальной скоростью 5 км/ч, а по лесу – с максимальной скоростью 3 км/ч. За какое наименьшее время пешеход сможет добраться из пункта А в пункт В?
Решение
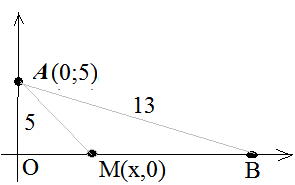
По теореме Пифагора OB = 12.
Надо решить задачу на условную оптимизацию 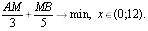
В координатах она имеет вид 
Приравняем производную нулю: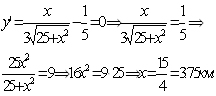
Производная меняет знак при переходе через эту точку с – на +, здесь точка минимума. Так как на интервале (0; 12) она единственная, то в этой точке достигается не только минимум, но и наименьшее значение. Подсчитаем затраченное время: 
4. [ЕГЭ 2006]. Пусть цена товара равна р рублей, а количество n проданного товара зависит от цены и выражается равенством n = 100 – p. При какой цене будет максимальной выручка?
Решение
Выручка будет равна y = (100 – p)p, то есть 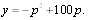
Зависимость квадратичная, при старшей степени коэффициент отрицательный, поэтому максимум достигается в вершине параболы. Ее абсцисса равна 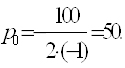
При такой цене товара будет продано n = 100 – 50 = 50 единиц, а выручка составит y = 50·50 = 2500 руб.
5. [4, с. 359].

6. [3, стр. 339]

Решение
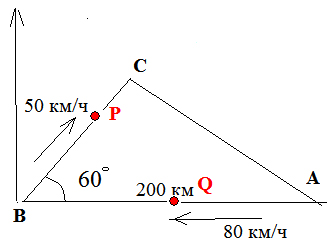
В момент времени t автомобиль будет в точке Q(200 – 80t, 0), а поезд – в точке 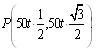
Квадрат расстояния равен 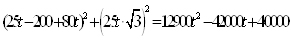
Получилась квадратичная зависимость, достигающая наименьшего значения в вершине с абсциссой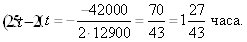 Подставляя в квадрат расстояния и извлекая корень, получаем примерно 76.25 км.
Подставляя в квадрат расстояния и извлекая корень, получаем примерно 76.25 км.
7. [11]

8. [11]

9. [11]

10. [11]

1. Panteleev F.V., Letova T.A. Metody optimizacii v primerah i zadachah:Ucheb. posobie.-M.: Vyssh. shk., 2002.
2. Tihomirov V.M.. Rasskazy o maksimumah i minimumah. - M.: Nauka, 1986 - (B-chka «Kvant». Vyp. 56).
3. Algebra i nachala matematicheskogo analiza: ucheb. dlya 10-¬11 kl. obscheobrazovat. uchrezhdeniy / [A.N. Kolmo¬gorov, A.M. Abramov, Yu.P. Dudnicyn i dr.]; pod red. A.N. Kolmororova. 17- ¬e izd. ¬ M. : Prosveschenie, 2008.
4. Mordkovich A.G. Algebra i nachala matematicheskogo analiza. 10-11 klassy. V 2 ch. Ch. 1. Uchebnik dlya uchaschihsya obscheobrazovatel'nyh uchrezhdeniy (bazovyy uroven') / A. G. Mordkovich. -10-e izd., ster. - M.: Mnemozina, 2009.
5. Alrebra i nachala analiza: ucheb. dlya 10-¬11 kl. obscheobrazovat. uchrezhdeniy / [Sh.A. Alimov, Yu.M. Kolyagin, Yu.V. Sidorov i dr.]. 15-¬e izd. ¬ M. : Prosveschenie, 2007.
6. Geometriya. 7-9 klassy : ucheb. dlya obscheobrazovat. uchrezhdeniy / [L.S. Atanasyan, V.F. Butuzov, S.B. Kadomcev i dr.]. -20-e izd. - M. : Prosveschenie, 2010.
7. Geometriya. 10-11 klassy : ucheb. dlya obscheobrazovat. uchrezhdeniy / [L.S. Atanasyan, V.F. Butuzov, S.B. Kadomcev i dr.]. -18-e izd. - M. : Prosveschenie, 2009.
8. Geometriya dlya 10-11 klassov : Ucheb. posobie uchaschihsya shk. i klassov s uglubl. izuch.matematiki/ A. D. Aleksandrov, A. L. Verner, V. I. Ryzhik. -3-e izd., pererab.- M. : Prosveschenie, 1992.
9. M.I.Bashmakov, Bekker B.M., Gol'hovoy V.M. Zadachi po matematike. Algebra i analiz /Pod red. D.K.Faddeeva. - M.: Nauka. Gl. red. fiz.-mat. lit., 1982 - (B-chka «Kvant». Vyp.22).
10. Kiselev A. P. Geometriya / Pod red. N.A. Glagoleva. - M.: Fizmatlit, 2004.
11. Lyashko I.I. Spravochnoe posobie po vysshey matematike. T.1: Matematicheskiy analiz: vvedenie v analiz, proizvodnaya, integral.-M.: Editorial URSS, 2001.






