Нижний Новгород, Россия
Нижний Новгород, Нижегородская область, Россия
Статья посвящена разработке формализованного представления организационной системы производственного предприятия с разнородными ресурсами и решает часть задач формирования механизма поддержки принятия решений его руководством в условиях необходимости оперативного увеличения объема выпускаемой продукции и сокращения сроков её поставки заказчику на основе эффективного использования имеющихся ресурсов. Объект исследования: организационная система промышленного предприятия, имеющего каскадную структуру жизненного цикла производства. Предмет исследования: абстрактные аспекты организационной системы как объекта формализованного ресурсного управления, способствующего снижению риска принятия нерациональных эвристических решений. Цель исследования: разработка графической математической модели организационной системы на основе ранее предложенных содержательной концепции и формализованных схем эффективного механизма ресурсного управления организационной системой. Методы: процессный и проектный подходы к управлению, методы аналогий и визуализации абстрактных описаний объекта управления, методы и средства описания импульсных технических систем. Основные результаты и их значимость: для отдельных стадий и всего цикла производства на основе развития принципов построения сетевых моделей объектов управления и расширения области применения моделей импульсных технических систем построены специализированные графы (сетевые модели), имеющие новые системные свойства. Предложены укрупненные графы, которые позволяют решить задачи диагностики ресурсного состояния организационной системы промышленного производства, выявить наличие и определить характер возможных проблемных ситуаций. Введены детализированные сетевые модели, которые необходимы для решения задачи ресурсного управления организационной системой, позволяют идентифицировать «входы» объекта управления – виды и параметры управленческих воздействий и отражают предпочтения двух видов лиц, принимающих решения – руководства предприятия и заказчиков выпускаемой продукции. В работе представлены правила вершин разработанных графовых моделей, приведены примеры их применения и определения численных параметров, показаны ограничения их возможностей.
модели организационных систем, промышленное производство, каскадная структура, разнородные ресурсы, производственно-импульсная аналогия, согласование фаз производства
Введение
Особенностью промышленного производства наукоемкой продукции (например, электронного приборостроения) является каскадная модель его фаз, представляющих разнородные (по виду производства [1]) технологические операции (количество которых измеряется сотнями) и требующих специализированных производственных ресурсов (оборудования, станков, оснастки). В терминах проектного подхода формальная связь указанных фаз соответствует типу «финиш-старт» [2]. При этом смежные фазы производства (ФП) в терминах процессного подхода взаимодействуют как «производитель» и «потребитель» промежуточных изделий [3]. Принципы бережливого производства диктуют выполнение требования поставки производителем продукции её потребителю в требуемом объеме и «точно в срок». Продукция, скопившаяся в незавершенном производстве вследствие различия производительностей в разных ФП и ожидающая своей очереди на следующие технологические операции, увеличивает стоимость конечного продукта и не позволяет сократить цикла производства, что ограничивает его эффективность [4]. Это обстоятельство требует решения задачи выравнивания производительностей (выработок) ресурсов во всех ФП [5].
Целью настоящей работы является построение модели организационной системы (ОС) предприятия как части математического обеспечения средств формализованной поддержки указанного решения.
Известные подходы к решению задачи выравнивания «загрузки» производственных ресурсов на практике сводятся к двум вариантам: эвристическому, при котором основное внимание ЛПР уделяется «расшивке» узких мест цикла производства, и формализованному ресурсному управлению, реализуемому специализированными автоматизированными системами (АС). Однако, первые из них эффективны лишь в условиях малых циклов производства – с количеством ФП не более 15-20, а вторые (например, АС Spider Project) – лишь для управления ОС с однородными ресурсами [6], [7], не характерными для рассматриваемой предметной области, что говорит об актуальности данной работы.
- Материалы, модели, эксперименты, методы и методики
Формирование математических моделей ОС выполним в соответствии со следующими подходами и исходными материалами:
- Математические модели являются абстракцией семантической концепции объекта моделирования [8], являющейся их основой. В рассматриваемом случае такой исходной теорией принята разработанная ранее парадигма управления ОС с разнородными ресурсами [5].
- Графическую интерпретацию парадигмы управления ОС с разнородными ресурсами, введенную в работе [6] в рамках перспективного направления моделирования на основе визуализации абстрактных представлений, целесообразно развить до уровня графических математических моделей.
- Предложенные в [7] формализованные схемы механизма управления ОС являются промежуточными результатами процесса моделирования, которые логично обеспечивают переход от семантической концепции к собственно моделям и будут применены в данной работе.
Для достижения поставленной цели в рамках выбранных методов и известных разработок необходимо решить следующие задачи: сформировать абстрактное описание исходного ресурсного состояния ОС, которое позволит определить критическую фазу, ограничивающую производительность производства, и степень рассогласования выработки ресурсов указанных фаз; обосновать структуру математической модели организационной системы как объекта управления и определить управляющие входы, состав исходных и выходных данных; определить параметры указанных моделей; продемонстрировать их возможности на практическом примере.
- Результаты
Модель исходного состояния организационной системы
Прежде чем формировать модель ОС как строгое абстрактное описание объекта управления предварительно составим укрупнённую модель исходного состояния ОС, описывающую проблему рассогласования выработки продукции в совокупности связанных производственных фаз, а затем определим численные параметры этой модели на простом демонстрационном примере [6], представленном в табл.1.
Таблица 1
Пример фаз – последовательных стадий технологического процесса, основного плана загрузки ресурсов и трудоёмкости технологических операций [6]
Table 1
An example of phases - successive stages of a technological process, a basic resource application plan and labor intensity of technological operations [6]
|
Виды производства |
||||
|
Заготовительное |
Обрабатывающее |
Химико-технологическое |
Сборочное |
Регулировка |
|
i=1 |
i=2 |
i=3 |
i=4 |
i=5 |
|
Основной план (5 рабочих дней по 8 час): длительность рабочей недели, мин/нед. |
||||
|
2400 |
2400 |
2400 |
2400 |
2400 |
|
Трудоемкость изготовления изделий по фазам, мин/шт. |
||||
|
156 |
170 |
284 |
208 |
120 |
С учетом ранее разработанных промежуточных этапов моделирования – визуальной интерпретации механизма управления ОС с разнородными ресурсами [6] и его формализованных схем [7] модель ОС с каскадным циклом производственных фаз предлагается представить в виде ориентированного двумерного графа с потоками, отличающимися от известных моделей импульсным характером с соответствующими временными параметрами. Такой граф для случая примера табл.1 (пяти последовательных ФП) представлен на рис. 1.
Здесь каждый путь от начальной до конечной вершины моделирует функционирование соответствующего ФП, причем выделенные три части графа (сети) имеют разные по смыслу моделируемых аспектов фаз потоки, которые поэтому также являются разнородными.
Свойства орграфа определяются правилами его вершин, которые приведены ниже.
а) Первая часть сети (рис.1) содержит вершину Т без входящих потоков. Вершина T с отрицательно инцидентными дугами 1,…,N (N – количество ФП) показана на рис.2. Правила вершины приведены в таблице 2, которая иллюстрирует свойства 1-й части сети (рис.1), а именно то, что потоки в каждой из отрицательно инцидентных вершине Т дуг, моделирующих фазы производства, одинаковы.
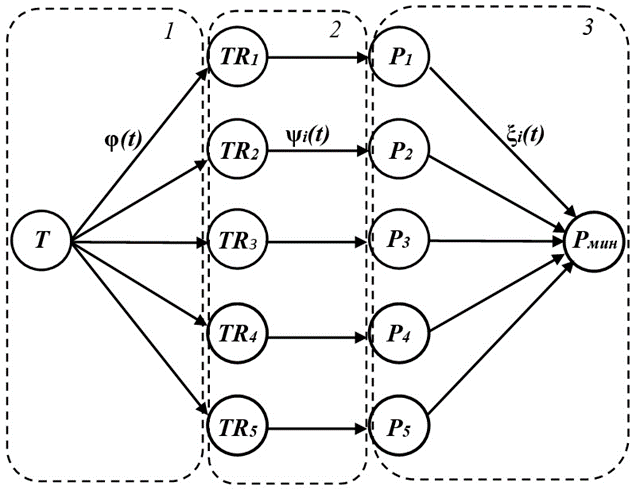
Рис.1. Модель исходного состояния ОС
Fig.1. Initial State Model of OS
Таблица 2
Правила Т-вершин
Table 2
T-vertex rules
|
Мощность вершины T |
Поток в дуге 1 |
Поток в дуге i |
Поток в дуге N |
|
τ |
φ(t)=1, 0≤ t≤ τ φ(t)=0, τ<t< t0 |
φ(t)=1, 0≤ t≤ τ φ(t)=0, τ<t< t0 |
φ(t)=1, 0≤ t≤ τ φ(t)=0, τ<t< t0 |

Рис. 2. Вершина T-типа
Fig. 2. T-type vertex
Физический смысл мощности вершины Т, а значит и потоков во всех инцидентных ей дугах, – длительность времени τ функционирования (выполнения работ) каждой ФП в интервале времени планирования [0,t0]. Поток в этих дугах можно представить в виде последовательности импульсов «включения» в работу ресурсов соответствующих ФП (рис.3,a).
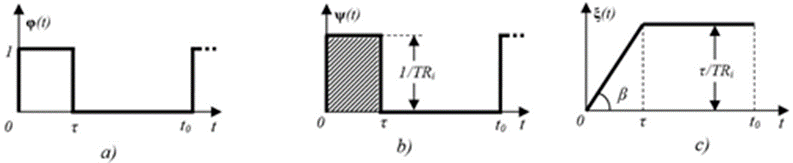
Рис. 3. Осциллограммы потоков графа (рис.1): поток дуг T-TR (а), поток дуг TR-Р (b) и поток дуг Р-Рмин (c)
Fig. 3. Oscillograms of graph flows (Fig.1): arc flow T-TR (a), arc flow TR-P (b) and arc flow P-Rmin (c)
б) Вторая часть графа (рис.1) содержит вершины TRi (i=1,…,N), смысл мощностей которых есть трудоемкости соответствующих ФП. Формальные правила TRi-вершины с инцидентными ей дугами (рис.4) представлены в табл. 3, вид потока в дуге 2 − на рис.3,b. Смысл параметра этого потока – «скорость изготовления» продукции (производительность ресурсов), выпускаемой конкретной ФП в промежутке времени [0,τ].

Рис. 4. TRi- вершина
с инцидентными ей дугами
Fig. 4. TRi- vertex with incident arcs
в) Третья часть сети (рис.1) содержит вершины Pi, мощность которых моделирует количество продукции, произведенной в разных ФП за промежуток времени [0,τ]. Формальные правила Pi -вершины (i=1,…,N) с инцидентными ей дугами (рис.5) представлены в таблице 4, вид потока в дуге 2 − на рис.3,с. Смысл потоков в отрицательно инцидентных вершинам Pi дугах есть количество продукции ξi(t), произведенной к моменту времени t в отдельных ФП.
Таблица 3
Правила TRi-вершин
Table 3
TRi-vertex rules
|
Поток в дуге 1 |
Мощность вершины TRi |
Поток в дуге 2 |
|
φ(t) |
TRi |
ψi(t) = φ(t)/ TRi |
Таблица 4
Правила Pi-вершин
Table 4
Pi-vertex rules
|
Поток в дуге 1 |
Мощность вершины Pi |
Поток в дуге 2 |
|
ψi(t) |
Pi = τ/ TRi |
ξi(t) = t·tgβ= t/TRi, 0≤t≤τ ξi(t) = τ/ TRi, τ<t≤t0 |
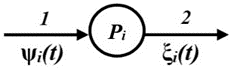
Рис. 5. Pi -вершина
с инцидентными ей дугами
Fig. 5. Pi -vertex with incident arcs
|
Таблица 4 - Правила Pi -вершины
|
Отметим, что функция ξi(t) при τ≤ t≤ t0 имеет величину, равную площади заштрихованного импульса на рис. 3,b.
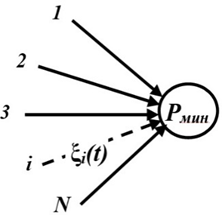
Рис. 6. Pмин - вершина с инцидентными дугами
Fig. 6. Pмин - vertex with incident arcs
г) Вершина Pмин без исходящих потоков (рис.1) завершает структуру графа. Физический смысл мощности этой вершины есть выработка всего цикла производства за период времени [0,t0], которую и моделирует вершина Pмин. Формальные правила вершины Pмин с инцидентными ей дугами (рис.6) представлены в таблице 5 (оператор E(х) возвращает целую часть х).
Для формализованной идентификации «узкого места», ограничивающего производительность цикла производства (описываемого сетевой моделью), целесообразно воспользоваться широко применяемым методом критического пути [9]. Его особенностью является путь на сети, который имеет наибольший параметр потока. Изменим признак критического пути. Поскольку в соответствии с графической интерпретацией концепции управления ОС [6] таким узким местом является фаза с наибольшей трудоемкостью, то критический путь правомерно определять по наибольшей мощности вершин TRi. А это, в свою очередь, означает, что искомый критический путь графа определяется исключительно его вершиной, находящейся во второй части графовой модели (рис.1) и имеющей максимальную мощность.
Практический пример модели исходного состояния организационной системы
Сформированную формальную модель исходного состояния ОС (рис.1) конкретизируем по исходным данным демонстрационного примера (табл.1) и правилам вершин (табл.2-5).
Полученный таким образом граф (вершины отмечены их мощностями) с выделенным критическим путем представлен на рис.7 (размерности мощностей Т- и TRi-вершин соответствуют табл.1, вершин Pi и Pмин – шт./нед.).
Критический путь, определённый по предложенному критерию, будет характеризовать ФП с наименьшей производительностью (критическая ФП), а конечная вершина графа, входящая в критический путь, моделирует тот факт, что выработка всего производственного процесса ограничена выработкой критической ФП (в примере – 8 шт./нед.). Представленная сеть (рисунки 1 и 7) моделирует факт рассогласования ФП и нарушения принципов бережливого производства, она показывает необходимость применения процедур управления, формализованный подход к которому требует разработки соответствующей модели объекта управления.
Таблица 5
Правила Pмин-вершины
Table 5
Pмин-vertex rules
|
Поток в дуге 1 |
Поток в дуге i |
Поток в дуге N |
Мощность вершины Pмин |
|
ξ1(t) |
ξi(t) |
ξN(t) |
Е(min{ τ/ TRi}), i=1,…,N |

Рис. 7. Графовая модель исходного состояния ОС, соответствующая данным табл.1
Fig.7. Graph model of the initial state of the OS, corresponding to the data in Table 1
Модель организационной системы как объекта управления
В решении задачи формализованного управления ОС предлагается развить известный принцип автоматизированного управления техническими импульсными системами (ТИС) [10], основанный на широтно-импульсной модуляции (ШИМ, в англоязычной литературе - PWM) [11,12], на область ОС, функционирование которых в рассматриваемой предметной области подобно процессам ТИС (см. рис.3). Так, при управлении ТИС на основе ШИМ управление сводится к целенаправленному изменению т.н. коэффициента заполнения [импульсной последовательности] k [10]. Для области ОС величину k предлагается численно определять следующим образом: k = τ/t0, а параметры модели τ и t0 при этом принимают смысл времени «задействования» (работы) ресурса организационной системы τ и его максимальной (установленной горизонтом оперативного планирования) величины t0 соответственно. В приведенном примере рассмотрен обычный (термин − по Трудовому Кодексу РФ) режим, тогда τ = 40 час/нед. (2400 мин/нед.), а максимально возможное рабочее время (сменный режим) работы оборудования в неделю («станки не выключают») t0 = 168 час/нед. (10080 мин/нед.). Таким образом очевидно, что в частном случае односменного (обычного) режима работа ресурсов ОС характеризуется одинаковой для всех ФП величиной коэффициента заполнения и равной k = 0,2381.
Модель ОС как объекта управления должна содержать вход, управляющий величиной k, целенаправленно изменяя которую (как это следует из рис. 3, b и с) дифференцированно для каждой ФП, возможно осуществить (с известными ограничениями [5,6]) равенство выработок во всех ФП. В состав входных данных модели входят трудоемкости TRi операций по каждой ФП (пример см. в табл.1). Поскольку затраты производства зависят от загрузки оборудования [2-4], входные данные модели должны включать сведения Ji по стоимости одного часа его работы для каждой ФП в зависимости от возможного времени загрузки (первая смена, сверхурочная работа, вторая, третья смены и т.д.), а также допустимую стоимость единицы (партии) продукции Cмакс. Выходы модели ОС должны отражать общую выработку P всего цикла производства за время t0, а также фактическую стоимость С единицы (партии) продукции (общую и детализированную по каждой ФП).
С учетом сказанного графовая модель ОС для пяти ФП примет вид, приведенный на рис.8.

Рис. 8. Графовая модель ОС как объекта управления
Fig.8. Graph model of the OS as a management object
Приведем правила вершин, отличающиеся от правил табл.2-5.
a) Мощность Т-вершины и потоки ее дуг моделируют период планирования t0.
б) Формальные правила τi-вершины с инцидентными ей дугами (рис.9) представлены в табл. 6.

Рис. 9. τ-вершина
с инцидентными ей дугами
Fig.9. τ-vertex with incident arcs
Таблица 6
Правила τi-вершин
Table 6
τi-vertex rules
|
Поток в дуге 1 |
Поток в дуге 2 |
Мощность вершины τ |
Поток в дуге 3 |
|
t0 |
ki |
ki* t0 |
ki* t0 |
в) Формальные правила Pi-вершины с инцидентными ей дугами (рис.10) представлены в таблице 7.

Рис. 10. Р-вершина
с инцидентными ей дугами
Fig.10. Р- vertex with incident arcs
Таблица 7
Правила Pi-вершин
Table 7
Pi-vertex rules
|
Поток в дуге 1 |
Поток в дуге 2 |
Мощность вершины Pi |
Поток в дуге 3 |
|
TRi |
ki* t0 |
ki* t0/ TRi |
ki* t0/ TRi |
г) Формальные правила Сi-вершины с инцидентными ей дугами (рис.11) представлены в таблице 8.

Рис. 11. Ci - вершина
с инцидентными ей дугами
Fig.11. Ci - vertex with incident arcs
Таблица 8
Правила Сi-вершин
Table 8
Сi-vertex rules
|
Поток в дуге 1 |
Поток в дуге 2 |
Мощность вершины Ci |
Поток в дуге 3 |
|
Ji |
ki* t0 |
Ji *ki* t0 |
Ji*ki* t0 |
Мощность внешней вершины Р равна минимальной мощности вершин Pi до выравнивания выработки ФП и одинаковым по величине мощностям Pi, (i=1,…,N) – после выравнивания. Мощность вершины С равна сумме мощностей вершин Сi, (i=1,...,N). Для удовлетворения запросов потребителя должно выполняться условие С≤ Cмакс.
Обсуждение/Заключение
- Новизна полученных результатов состоит в том, что, в отличие от известных графовых моделей с потоками, впервые введены графы с потоками в виде последовательности импульсов, что позволяет реализовать ресурсное управление ОС на основе принципа ШИМ аналогично автоматическим средствам управления в технических системах, управляя дифференцированной для каждой фазы производства величиной коэффициента заполнения указанной последовательности.
- Полученные результаты моделирования, проиллюстрированные на практических примерах, показывают целесообразность и возможность применения развитых в работе графовых моделей для формализованного описания организационных систем и в задаче их диагностики, и в задаче управления их разнородными ресурсами.
- Предлагаемый подход имеет принципиальное ограничение по величине предельной выработки процесса производства − она лимитируется максимальной величиной коэффициента заполнения (kмак=1) для той ФП, которая характеризуется наибольшей трудоемкостью технологического процесса.
- В работе представлены графовые модели ОС как объекта управления, задачи разработки формализованного механизма управления на основе этих моделей являются темой следующего исследования.
1. ГОСТ 14.004-83. Технологическая подготовка производства. Термины и определения основных понятий. М.: Стандартинформ, 2009. 9 с.
2. Project Management Standard and Guide to the Project Management Body of Knowledge, 7th Edition. Newtown Square, Pennsylvania: Project Management Institute, Inc, 2021. 274 р. ISBN 9781628256673.
3. Наугольнова И.А. Процессный подход к управлению: эволюция, современные вызовы, инновации // Креативная экономика. 2023. Т. 17, № 6. С. 2143−2164. DOIhttps://doi.org/10.18334/ce.17.6.117951. EDN CZJASG.
4. Droup I., Jusoh A., Mardani A., Nor Kh.Md., Dafa' A., Alla N.A. The impact of lean manufacturing practices on firms’ sustainable performance of the manufacturing industry sector. International Journal of Public Sector Performance Management. 2022;10(2/3):283−301. DOIhttps://doi.org/10.1504/IJPSPM.2022.126234.
5. Ивлев М.А., Рябов Д.Е. Разработка концепции повышения эффективности организационных систем мультипроектного научно-производственного предприятия // Современные наукоемкие технологи. 2024. № 2. С. 20–25. DOIhttps://doi.org/10.17513/snt.39926. EDN HFXJFD.
6. Ивлев М.А., Рябов Д.Е. Визуальная интерпретация парадигмы управления организационной системой с разнородными производственными ресурсами // Эргодизайн. 2024. №3 (25). С. 271–279. DOIhttps://doi.org/10.30987/2658-4026-2024-3-271-279. EDN GOZKOQ.
7. Ивлев М.А., Рябов Д.Е. Формализованные схемы механизма управления организационной системой, реализующей циклы производства как совокупность разнородных бизнес-процессов // Экономика. Право. Инновации. 2024. №3. С. 38–46. DOIhttps://doi.org/10.17586/2713-1874-2024-3-38-46. EDN CDHDPL.
8. Месарович М., Такахара Я. Общая теория систем. М.: Мир, 1978. 307 с.
9. Desticioğlu B. Project planning with CPM and PERT methods: example of defense industry. Journal of Naval Sciences and Engineering. 2022;18(2):363−385.
10. Коломейцева М.Б., Беседин В.М., Ягодкина Т.В. Основы импульсной и цифровой техники: учебное пособие для вузов. 2-е изд., испр. и доп. М.: Издательство Юрайт, 2024. 124 с. ISBN 978-5-534-06429-2.
11. Kurniawan A.D., Radianto D., Luqman M. Design of single phase inverter with pulse width modulation control system using fast PWM. Jurnal Elektronika dan Otomasi Industri. 2024;11(1):169−180. DOIhttps://doi.org/10.33795/elkolind.v11i1.4404.
12. Lee W., Kim T. Mode-change PWM method for improving efficiency of 3-level T-type PWM converter. Journal of Electrical Engineering and Technology. 2022;17(1):437−445. DOIhttps://doi.org/10.1007/s42835-021-00894-3.














