АВ статье рассматривается вопрос применения практических и методических приемов успешного и разнообразного формирования математической речи учащихся общеобразовательных учреждений. Приведены классификация методов формирования и конкретные примеры к каждому методу, а также некоторый теоретический материал.
методика преподавания математики, математическая речь, формирование речи, практические приемы
Формирование культуры речи - это повседневная работа над речью на всех уроках.
Труднее это дается на уроках математики.
В словаре С.И. Ожегова математика определяется как наука, изучающая величины, количественные отношения и пространственные формы. Характерная черта математики - широкое применение в ней специальных знаков, символов, позволяющих точно и обобщенно выражать соответствующие формы мыслей, поэтому ее справедливо называют особым языком. Следует помнить, что развитие мышления невозможно без развития речи. И наоборот, развивать речь без развития мышления - значит, прежде всего, воспитывать умение говорить, не заботясь о содержании.
Математическая речь является средством выражения математических мыслей, их образования и развития. Она подчиняется всем правилам речи, которые мы знаем из русского языка. Развитая речь - это содержательная, связная и правильная речь, это умение грамотно излагать полученные знания и выражать свои мысли.
Изложение школьного курса математики основано на совместном использовании словесной и символико-графической форм описания учебного материала. Каждая из этих форм - это своеобразный язык, служащий для передачи информации. Поэтому добиться осознанного и точного понимания учебного материала можно лишь при условии одинаково высокой подготовки школьников к восприятию информации, закодированной каждым из этих способов. Однако практика работы в школе убеждает нас в том, что пока еще многие учащиеся находятся в зависимости от формы подачи информации.
Методически умелое использование математического языка обеспечивает сознательность учения, ускоряет развитие мышления как совокупности логических операций, способности к дедуктивным рассуждениям, рациональному оперированию знаковыми системами, пространственным представлениям, запоминанию и воображению.
Традиционно проблемой формирования культуры речи занимаются специалисты в области русского языка, а также теории и методики обучения русскому и иностранным языкам. Однако указанная проблема на протяжении многих десятилетий была в центре внимания не только специалистов по русскому языку, но также и математиков, и специалистов по методике математики. В разное время проблемой формирования культуры речи учащихся при обучении математике занимались И.А. Гибш, А.Г. Мордкович, А.Я. Хинчин и др. Они рассматривали развитие речи в процессе обучения математике в тесной связи с формированием культуры мышления.
И.А. Гибшу принадлежат ставшие уже классическими исследования по развитию речи школьников при обучении математике. До настоящего времени большую ценность представляют как его методические рекомендации по развитию речи, так и данная им классификация ошибок и недочетов, наблюдающихся в устной и письменной математической речи учащихся.
А.Я. Хинчин исследовал указанную проблему как часть общей проблемы преодоления формализма математических знаний.
А.Г. Мордкович говорит о развитии речи на уроках математики как об особой цели математического образования, что нашло отражение в разработанных под его руководством учебно-методических комплектах по алгебре для 7-11 классов.
В таблице 1 приведены приемы формирования культуры математической речи учащихся.
Таблица 1
| Вид математической речи | Прием формирования | Характеристика приема | Пример использования приема |
| Устная математическая речь | Работа над звуковой стороной речи | Сводится к формированию правильного произношения и выразительного чтения математических терминов и любого задания | 1. Исправьте неправильное предложение «Необходимо поменять знаки». («Необходимо изменить знаки») 2. Прочитайте правильно: прибавить к 95, вычесть из 89, к 139 прибавить 324 |
| Словарная работа | Сводится к пониманию и умению объяснять значение математических терминов, усвоению их правильного написания и формированию умений составлять содержательное связное высказывание | 1. Объясните значение слов и выражений: функция, аргумент, равенство, разрядное число, разрядные слагаемые, геометрия. 2. Запишите слова, вставив пропущенные буквы: нум.рация, выч.таемое, ед.ница, кил.грамм, п.добие, тр.угольник. 3. Упражнения на составление правильных связных высказываний: а) прочитайте предложение, вставив пропущенные слова: «Чтобы к числу прибавить сумму, можно к числу прибавить... слагаемое, а потом к полученному результату... .... слагаемое»; б) используя данные слова и выражения, составьте известное вам правило: слагаемое, сумма, найти, вычесть, неизвестное, слагаемое, другое, чтобы, надо, из |
|
| Культура речи | Сводится к устранению грамматических и математических ошибок, таких речевых недостатков, как неточность и бедность речи, употребление лишних слов, неправильный порядок слов в предложении и т.п. | 1. Упражнения на устранение грамматических и математических ошибок: а) устраните математические ошибки в тексте: «Чтобы найти неизвестное число в выражении х+2=8, надо к 8 прибавить 2»; б) на вопрос учителя Коля ответил так: «При прибавлении к цифре 5 числа 4 будет 9». Какие ошибки допустил Коля? 2. Упражнения на устранение речевых недостатков подбираются в основном такие же, как и на уроках чтения, только используется математический материал: «Пример 295+12=307 Коля прочитал так: «К двести девяносто пять прибавим 12 и получим триста семь». Правильно ли он прочитал?» |
|
| Связная математическая речь | Осуществляется в соответствии с требованиями к развитию речи на уроках литературы. | 1. Составьте текст, используя набор слов и выражений: «Чтобы, на, произведение, двух чисел, это, умножить, число, можно, умножить, первый, число, на, множитель, число, на второй, и, полученное, умножить, множитель». 2. Закончите объяснение: «Чтобы разделить число 12 на произведение 3·2, можно 12 разделить на... и ...» |
|
| Письменная математическая речь | Оформление в виде связного текста | Приемы формирования культуры письменной математической речи характеризуются наглядностью, доступностью к пониманию и компактностью материала | Примеры использования приемов формирования письменной речи приведены ниже |
| Оформление в виде рисунка | |||
| Оформление в виде схематического решения-рисунка | |||
| Оформление в виде схемы | |||
| Оформление в виде содержательной схемы | |||
| Оформление с применением символики | |||
| Оформление с помощью схемы-графа | |||
| Оформление в виде таблицы |
1. Оформление в виде связного текста
Задача. Первую половину рукописи машинистка перепечатывала по 6 страниц в час, а вторую половину - по 12 страниц в час. Сколько страниц в среднем печатала машинистка за 1 час?
Решение. На одну страницу из первой половины машинистка затрачивала 10 минут, а на одну страницу из второй половины - 5 минут. Значит, 2 страницы всей рукописи она перепечатывала в среднем 15 минут, что составляет ¼ часа. Отсюда, всего за один час в среднем машинистка перепечатывала 2·4 = 8 страниц.
Ответ. 8 страниц.
2. Оформление в виде рисунка
Задача. Взяли 6 листков бумаги и некоторые из них разорвали на 7 частей; некоторые из получившихся листков снова разорвали на 7 частей и так сделали еще несколько раз. Сосчитав общее число получившихся листков бумаги, установили, что их 67. Как показать, что произошла ошибка при подсчете?
Решение.
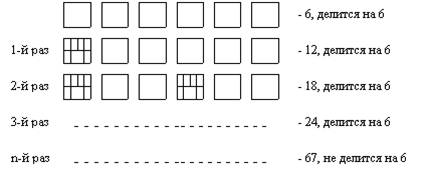
Ответ. Доказано, что произошла ошибка при подсчете.
3. Оформление в виде схематического решения-рисунка
Задача. Покажите, что 6 достаточно круглых, не отточенных карандашей можно расположить так, чтобы любые два из них соприкасались друг с другом.
Решение.

Ответ. Решение оформлено в виде схематического решения-рисунка.
4. Оформление в виде схемы
Задача. Из Москвы в Астрахань каждый день в 12.00 отправлялся теплоход, который находился в пути 4 суток. Из Астрахани в Москву ежедневно в 12.00 также отправлялся теплоход, который находился в пути 5 суток. Сколько теплоходов Астрахань-Москва встречал теплоход, отправлявшийся из Москвы, в течение всего пути?
Решение. Оформлено в виде схемы.
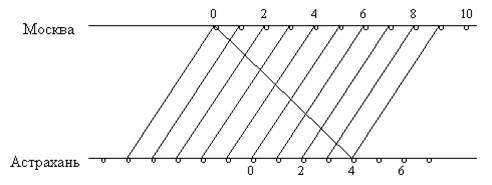
Ответ. 10 теплоходов.
5. Оформление в виде содержательной схемы
Задача. Колхознику необходимо прибыть в пункт, находящийся на расстоянии 134,7 км от его дома. 2,4 часа он ехал на автобусе со скоростью 55 км/ч, а остальную часть пути он шел пешком со скоростью 4,5 км/ч. Сколько времени он шел пешком?
Решение. Оформлено в виде содержательной схемы.
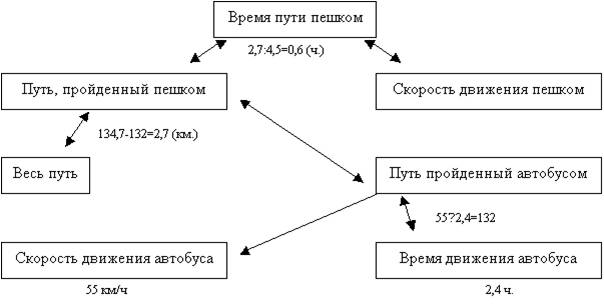
Ответ. 0,6 часа.
6. Оформление с применением символики
Задача. По дороге шли два отца, два сына и дедушка с внуком.
Сколько человек шло по дороге?
Решение. Одно из возможных решений, оформленное с применением символики, выглядит так:
{д, о} U {o, c} U {д, с} = {д, o, c},
где U - обозначение объединения множеств.
Обозначили: д - дедушка, о - отец, с - сын.
Ответ. 3 человека.
7. Оформление с помощью схемы графа
Графом называют схему (сетку, карту), составленную из нескольких точек, называемых вершинами графа, и нескольких отрезков (или дуг), соединяющих эти точки и называемых ребрами графа.
Задача. Сколько всевозможных примеров на деление (без остатка) можно составить с числами 12, 26, 4, 96, 13, 78 и 3?
Решение. Каждая выходящая стрелка - один пример. Петля при вершине графа означает примеры вида 12:12.

Ответ. 16 примеров.
8. Оформление в виде таблицы
Задача. Ходжа Насреддин расплачивался за ночлег в харчевне с ее хозяином ежедневно одним звеном золотой цепочки из семи одинаковых звеньев, чтобы не терять лишнее золото при распиливании, хозяин поставил Ходже условие: распилить только одно звено цепочки. Ходжа Насреддин с этим условием согласился и сумел его выполнить. Как он это сделал?
Решение.
| Дни | Отдал n-е звено | Получил n-е звено |
| 1 2 3 4 5 6 7 |
n=5 |
- n=5 - n=5,6,7 - n=5 - |
Ответ. Ходжа распилил 5-е звено цепочки.
1. Введенская Л.А. Русский язык и культура речи [Текст] / Л.А. Введенская, М.Н. Черкасова. - Ростов-на-Дону: Феникс, 2004. - 384 с. EDN: https://elibrary.ru/QQXYMD
2. Гибш И.А. Развитие речи в процессе изучения школьного курса математики [Текст] / И.А. Гибш // Математика в школе. - 1995. - № 6. - С. 2-5.
3. Гладкий А.В. Язык, математика и лингвистика [Текст] / А.В. Гладкий // Математика в школе. - 1994. - № 1. - С. 2-9.
4. Гнеденко Б.В. Развитие мышления и речи при изучении математики [Текст] / Б.В. Гнеденко // Математика в школе. - 1991. - № 4. - С. 3-9.
5. Фридман Л.М. Теоретические основы методологии обучения математике [Текст]: пособие для педагогов, методистов и педагогов высших учебных заведений / Л.М. Фридман. - Москва: Либроком, 2009. - 248 с.






