Россия
В статье рассматривается способ визуализации исходных данных и создание математической модели с целью определения оптимального решения. Производится выбор уже имеющейся визуальной модели с целью ее модификации и дополнения математической моделью. Предлагается выбор «карты аргументов», и приводятся необходимые алгоритмы. Демонстрируется пример визуально-математической модели.
принятие решений, математическая модель, визуальная модель, карта аргументов
Введение
Современная начертательная геометрия – это уже не просто «грамматика чертежа», но теоретическая и методологическая основа методов визуализации информации. Причем, она с успехом решает свои задачи не только если информационная модель может быть отображена на трехмерное евклидово пространство. В настоящее время методы начертательной геометрии с успехом вступают в область многомерных и неевклидовых пространств [1–4], что делает возможной визуализацию информационных моделей, приводимых к таким пространствам. Тем не менее все эти примеры демонстрируют возможности визуализации в отношении лишь одного типа информационных моделей – на основе так называемой количественной информации. Визуализация качественной информации задействует иные математические абстракции (в первую очередь, графы), казалось бы, не имеющие непосредственного отношения к начертательной геометрии.
В высшем техническом образовании начертательная геометрия присутствует тоже не сама по себе, а как составляющая графического цикла – начертательная геометрия, инженерная и компьютерная графика. Под этим длинным названием в действительности скрываются элементы дисциплины, которая называется прикладной (инженерной) геометрией. Отметим, что в круг вопросов инженерной графики входит построение схем (структурных, функциональных, принципиальных и пр. – ГОСТ 2.701), а схемы, в свою очередь, являются разновидностью графовых моделей, т.е. информационных моделей качественного типа. Также отметим, что уже в 60–70-х гг. XX в. в отечественной школе прикладной геометрии ставился вопрос о включении теории графов в круг вопросов дисциплины [5].
Сказанное позволяет сделать следующее обобщение. Инженерная геометрия вправе включить в круг своих проблем разработку графических моделей, изоморфных различным информационным моделям не только количественного, но и качественного, и гибридного типов, т.е. проблемы визуализации информации, в целом.
Созданию визуальной модели такого типа посвящена настоящая статья.
1. Задача оценки и принятия решения встает перед всяким человеком, не важно руководит он организацией, отделом или выбирает автомобиль, готовится в отпуск, ищет работу или собирается записаться на курсы по вождению. И очень часто в принятии решений человеку требуется помощь, подсказка. Поэтому на практике широко применяются методы поддержки принятия решений, в частности, визуальные средства – таблицы, диаграммы, схемы [1].
Наглядность – одна из особенностей визуального моделирования, которая позволяет либо сразу увидеть решение, либо получить подсказку для его нахождения. Наглядная модель способствует коммуникации и передаче знаний, а также общению между специалистами. Однако в условиях принятия решений возникает вопрос о полном представлении и объективном понимании проблемы, которую предстоит разрешить. На помощь приходят, например, диаграмма Исикавы, карта аргументов или Квадрат Декарта. Главным недостатком существующих визуальных моделей является невозможность дать объективную (количественную) оценку решению, качественно представленному при помощи той или иной визуальной модели.
Поэтому разработка визуальных моделей для поддержки принятия решений, которые к тому же давали возможность проводить количественную оценку принимаемого решения, является актуальной проблемой.
Целью настоящей работы является создание визуальной и математической модели для объективного представления особенностей принятия решения с учетом всех достоинств и недостатков.
2. Разработка визуальной модели.
В качестве основы возьмем существующую визуальную модель – диаграмму «Карта аргументов» [2]. Карты аргументов применяются для визуального преставления хода размышлений или дискуссий. Вверху диаграммы помещают тему дискуссии, вниз от нее ответвляют высказывания – положительные (аргументы «за»), отрицательные (аргументы «против») и нейтральные. К каждому высказыванию применяют те же правила. Для наглядности знак аргумента выделяют цветом: зеленый – «за», красный – «против», серый – нейтральное высказывание (рис. 1,а).
В задаче принятия решений «темой» является принимаемое решение, «высказываниями» − аргументы «за» (плюсы решения) и «против» (минусы решения). Нейтральные высказывания не предполагаются. Каждый аргумент итерационно может быть расщеплен на подаргументы.
Пусть аргументы выбираются не случайно, а в ходе последовательного анализа принимаемого решения. В этом случае, как правило, их можно разделить на условные группы. Примерами таких групп являются «большие кости» на диаграмме Исикавы (рис. 1,б) [1]. Расположение элементов на диаграмме Исикавы недостаточно системно, что не позволяет использовать ее для визуализации количественных оценок, поэтому будем располагать группы аргументов, как это делается при составлении денотатного графа (рис. 1,в) [1].

а) б) в)
Рис. 1. Некоторые существующие диаграммы:
а – карта аргументов, б – диаграмма Исикавы, в – денотатный граф
Окончательная визуальная модель строится на равномерной (не обязательно квадратной) сетке и представляет собой следующее (рис. 2). Верхний блок диаграммы – принимаемое решение, его размеры произвольны. Под ним располагаются группы аргументов (критерии анализа). Их высота одинакова, а ширина определяется приоритетностью критерия: тем больше, чем важнее критерий. Под критериями помещаются его плюсы (зеленые блоки) и минусы (красные блоки). Ширина блоков равна ширине блока критерия, высота – определяется значимостью аргумента: чем более значим, тем больше высота.
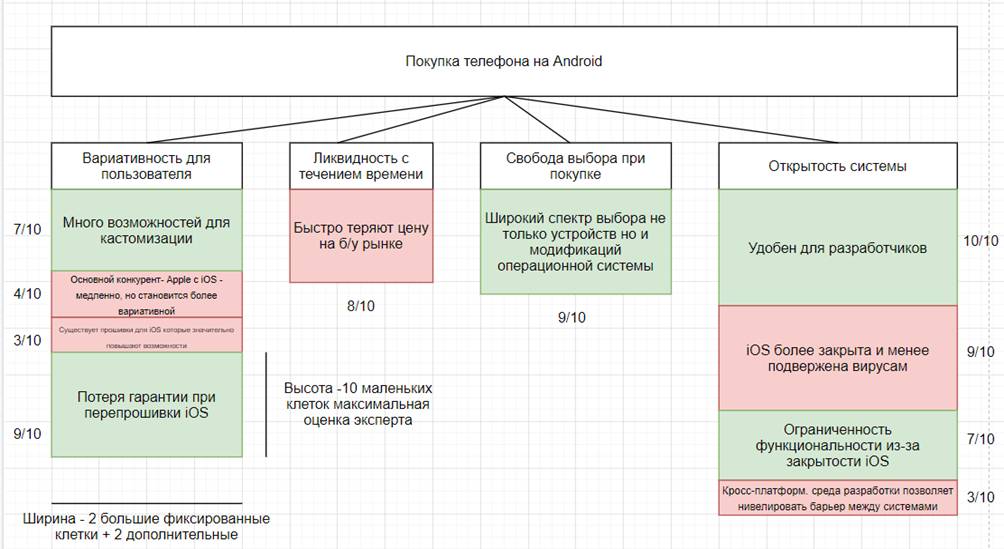
Рис. 2. Пример визуальной модели с возможностью количественной оценки
3. Разработка математической модели (количественные характеристики модели).
Изменяемыми параметрами модели являются ширина блоков критериев и высота блоков аргументов. Для их управления введены экспертные оценки – приоритетность (P) для критериев и значимость (W) для аргументов.
Приоритетность – значение в диапазоне от 1 до Pmax. Если ширину блока критерия (фактически, столбца) брать равной P, то на квадратной сетке столбцы оказываются узкими для любых значений P.В этом случае текст следует размещать вертикально. Для горизонтального текста требуется прямоугольная сетка или масштабная компенсация по ширине. Кроме того, при малых значениях P столбцы все равно оказываются слишком узкими. С учетом сказанного, ширину столбца определяет следующее выражение:
h = w0·(K+P),
где K – число условных клеток, «выравнивающих» ширину столбца для малых значений P, w0– масштабная ширина клетки.
Значимость – значение в диапазоне от 1 до Wmax. Значение Wmax выбирается исходя из удобства выбора экспертной оценки, например, 1–5 или 1–10. Аргументы с 0-вой значимостью не рассматриваются. Высоту ячейки аргумента определяет выражение:
h = h0·W,
где h0 – масштабная высота клетки.
Диаграмма на рис. 2 построена при следующих значениях констант: K=2, Pmax=3, w0=4, Wmax=10, h0=1.Определяем ширины столбцов. Так, приоритетность первого критерия («вариативность») составляет P1=2, ширина столбца – w1=4(2+2)=16 клеток, второго («ликвидность») P2=1 и w2=4(2+1)=12 клеток, последнего («открытость») P4=3 и w4=4(2+3)=20 клеток. Высоты блоков точно равны значению значимости Wi.
Количественную оценку анализируемого решения (M) будем определять по формуле:
M=∑Wi/Wmax·Pi,
где Wi берется с учетом знака (аргументы «за» – знак плюс, «против» – минус).
В приведенном примере
M=
(1 столбец) (7+9 – 4 – 3)/10·Pi [= 9/10·Pi = 0.9·2 = 1.8 ] +
(2 столбец) –8/10·Pi [=–0.8·1 = –0.8 ] +
(3 столбец) 9/10·Pi [= 0.9·2 = 1.8 ] +
(4 столбец) (10+7 – 9 – 3)/10·Pi [= 5/10·Pi = 0.5·3 = 1.5] =
1.8 – 0.8 + 1.8 + 1.5 = 4.3
Рассматривая интервал (–1.5; 1.5) как интервал «больших противоречий» (аргументы «за» и «против», в целом, уравновешивают друг друга), в примере мы видим, что решение является уверенно положительным.
Введем еще один количественный показатель – визуальную оценку (R), которая складывается как отношение большей из видимых площадей зеленого и красного цвета (зоны «за» и зоны «против») к меньшей: R = ∑+hiwi/ ∑–hiwi(∑+hiwi>∑–hiwi).
Для примера визуальная оценка составит: R = 740 / 448 ≈1,65, т.е. площадь «положительных» блоков более чем в 1,5 раза превышает площадь «отрицательных».
Поскольку площадь каждого блока при K≠0 оказывается завышена на величину hi·w0·K, что в сумме дает w0·K·∑hi, тогда визуальная оценка окажется не вполне достоверной. Оценим влияние выравнивающих клеток. Для этого рассчитаем отношение «чистых» площадей. В приведенном примере ∑+hi=7+9+9+10+7=42, ∑–hi=4+3+8+9+3=27, т.е. Δ= (740 – 4·2·42) /·(448 – 4·2·27)= 404 / 232 ≈1,74... Влияние составило около 10%, причем оценка оказалась занижена.
Чтобы избежать влияния выравнивающих клеток на R, столбцы следует окрашивать двумя цветами – серым (выравнивающая зона шириной w0·K) и зеленым / красным в зависимости от знака аргумента (все остальное). Наглядность в этом случае заметно снижается (красные и зеленые пятна оказываются разделены серыми), поэтому, пренебрегая влиянием выравнивающих клеток, можно использовать простую визуальную оценку.
Другими приемами, повышающими наглядность диаграммы, может служить перемещение столбцов, преимущественно зеленых, – влево, а преимущественно красных – вправо, а также перемещение блоков внутри столбцов так, чтобы зеленые собирались в верхней части столбцов, а красные – в нижней (рис. 3).
Заключение. В работе предложена визуальная (графическая) модель, изоморфная информационной модели в одной задаче принятия решений. Она может использоваться как средство визуализации и инструмент в принятии решений. Предложенная модель обладает наглядностью и легко может быть запрограммирована.


Рис. 3. Варианты расположения блоков для повышения наглядности
1. Гирш А.Г. Операция пересечения на комплексной плоскости // Геометрия и графика. -2021. - Т. 9. - №1. -С. 20-28. -DOI:https://doi.org/10.12737/2308-4898-2021-9-1-20-28
2. Гирш А.Г. Окружности на комплексной плоскости // Геометрия и графика. - 2020. -Т. 8. - №4. - С. 3-12. - DOI:https://doi.org/10.12737/2308-4898-2021-8-4-3-12
3. Абдурахманов Ш.А. Применение механизмов, отмечающих центры тяжестей симплексов в их 2-мерных проекциях как аксонографов многомерных пространств // Геометрия и графика. - 2020. - Т.8. - №4. - С. 13-23. - DOI:https://doi.org/10.12737/2308-4898-2021-8-4-13-23
4. Волошинов Д.В. Алгоритмический комплекс для решения задач с квадриками с применением мнимых геометрических образов // Геометрия и графика. - 2020. -Т. 8. - № 2. - С. 3-32. - DOI:https://doi.org/10.12737/2308-4898-2020-3-32
5. Четверухин Н.Ф. Прикладная геометрия и некоторые вопросы ее развития / Н. Ф. Четверухин // Прикладная геометрия и инженерная графика. - Киев: Будівельник, 1969. - Вып. 8. - С. 3-6.
6. Tufte E.R. The Visual Display of Quantitative Information. 2nd edition. - Cheshire, CT: Graphics Press, 2001. - 199 p.
7. BexF. J., Modgil S.,Prakken H., Reed Ch. On logical specifications of the Argument Interchange Format // Journal of Logic and Computation. - 2013. - 23 (5). - pp. 951-989. doihttps://doi.org/10.1093/logcom/exs033






