с 01.01.2016 по настоящее время
Екатеринбург, Владимирская область, Россия
Россия
Казань, Республика Татарстан, Россия
УДК 69 Строительство. Строительные материалы. Строительно-монтажные работы
ГРНТИ 67.11 Строительные конструкции
ГРНТИ 67.01 Общие вопросы строительства
ОКСО 270000 АРХИТЕКТУРА И СТРОИТЕЛЬСТВО
ББК 385 Строительные конструкции
ББК 308 Монтаж, эксплуатация, ремонт машин и промышленного оборудования
BISAC TEC005000 Construction / General
В статье предложена методика учета высших форм колебаний при оценке сейсмостойкий систем с эластомерными опорами на воздействия уровня «Максимальное расчетное землетрясение». В рамках исследования выполнен комплекс динамических и статических расчетов в нелинейной постановке с целью верификации предложенной методики нахождения модифицированной системы сил. Установлено, что расчет на сейсмические воздействия уровня МРЗ систем с эластомерными опорами возможно выполнять на основании предложенного модифицированного нелинейного статического метода. Полученные результаты соответствуют результатам, полученным на основании прямого динамического метода.
сейсмостойкость, расчет на максимальное расчетное землетрясение, ККСК, Pushover-анализ
1 Введение
Ежегодно в мире происходит порядка 300 тысяч землетрясений. Эпицентр большинства из них находится вдали от населенных пунктов, а магнитуда воздействия достаточно мала. Однако некоторые землетрясения оказывают катастрофические воздействия на целые города, разрушая их и нанося колоссальный экономический ущерб. Таким образом, повышение сейсмостойкости зданий и сооружений – одна из самых актуальных проблем при строительстве в сейсмически опасных зонах.
Тривиальным решением обеспечения сейсмостойкости сооружений является увеличение жесткости несущих элементов за счет увеличения их размеров (пассивная сейсмозащита), что приводит к увеличению инерционных нагрузок на рассматриваемое сооружение. Таким образом, данное решение не всегда является рациональным и экономически целесообразным.
Еще в 60-е годы ХХ века был предложен альтернативный способ повышения сейсмостойкости систем – сейсмоизоляция (активная сейсмозащита). Сам термин сейсмоизоляция обозначает снижение инерционных сил, вызванных сейсмическим воздействием, путем введения в систему «Основание – Динамическая модель» специальных элементов, позволяющих снизить инерционные нагрузки на систему. На Рисунке 1 представлены деформирование схемы здания без сейсмоизоляции и с ее применением. Благодаря большей податливости в нижней части системы горизонтальные перемещения, в целом, возрастают при уменьшении ускорения масс.
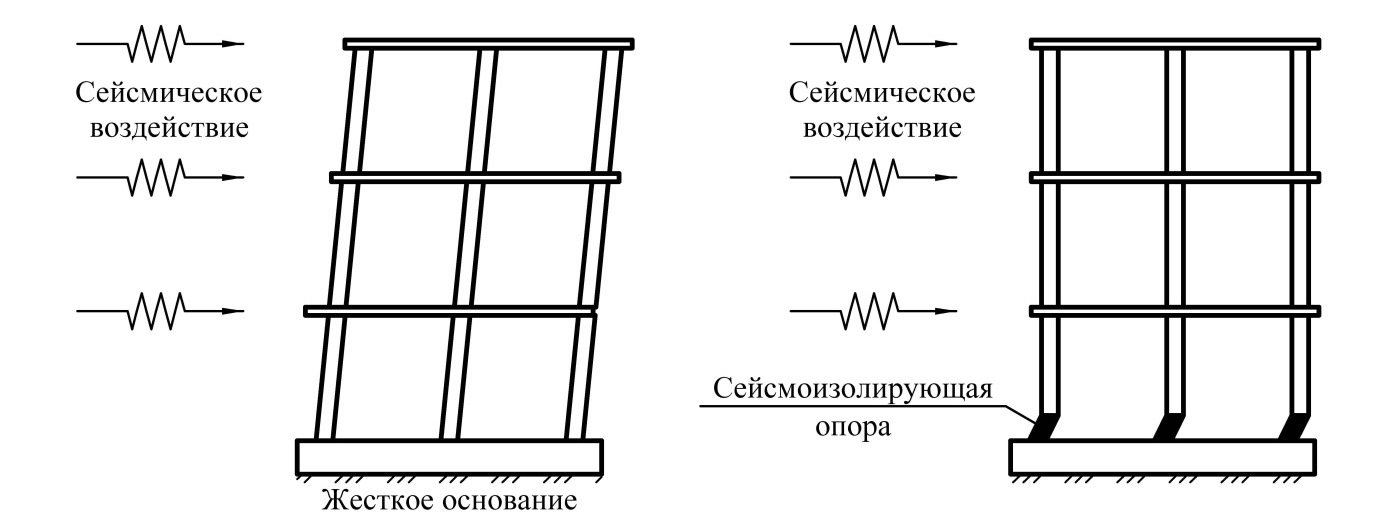
Рисунок 1 – Деформированная схема здания: а) – здание без сейсмоизоляции; б) – зданий и сейсмоизоляцией
Согласно СП 14.13330 оценка сейсмостойкости при сейсмическом воздействии уровня «Максимальное расчетное землетрясение» выполняется на основании прямого динамического метода путем интегрирования уравнений движения во временной области с использованием набора инструментальных записей ускорений основания при землетрясениях, наиболее опасных для сооружения, или синтезированных акселерограмм (рисунок 2). Такие расчеты требуют большого временного ресурса, сложного программного обеспечения и специальной квалификации проектировщика.

Рисунок 2 – Акселерограмма горизонтальной компоненты землетрясения, Iran, 1978 г.
Альтернативой прямого динамического расчета является нелинейный статический метод – Pushover analysis, при котором конструкция подвержена монотонно возрастающим горизонтальным усилиям. Согласно [7], [8] для оценки сейсмостойкости системы необходимо выполнить как минимум два расчета с различным распределением инерционных горизонтальных сил по высоте системы:
- Система инерционных сил, соответствующая главной форме собственных колебаний системы. Оценку сейсмостойкости системы с заданным распределением возможно выполнить только если модальная масса рассматриваемой формы не менее 75%;
- Система инерционных сил, полученная на основании суперпозиции инерционных сил нескольких форм колебаний. При этом суммарная модальная масса рассматриваемых колебаний не должна быть меньше 90%;
- Универсальное распределение системы сил пропорционально сосредоточенным массам в узлах системы;
- Адаптивная система инерционных сил, изменяющаяся в зависимости от перемещения узлов системы в процессе нагружения.
Дальнейший поиск характеристической точки на графике несущей способности системы (рисунок 3), посредством которой оценивается сейсмостойкость системы – процесс трудоемкий и требующий построения громоздких графиков и нетривиальных вычислений. В современных программных комплексах реализован нелинейный статический метод только на основании системы инерционных сил, соответствующей только одной из форм колебаний. Кроме того, отклик конструкции при заданном воздействии значительно меньше результатов, полученных на основании прямого динамического метода, на основании которого возможно наиболее точно оценить отклик конструкции на заданное сейсмическое воздействие. Несомненным преимуществом нелинейного статического метода является значительная экономия времени машинного расчета и трудоемкости оценки сейсмостойкости по сравнению с прямым динамическим методом.
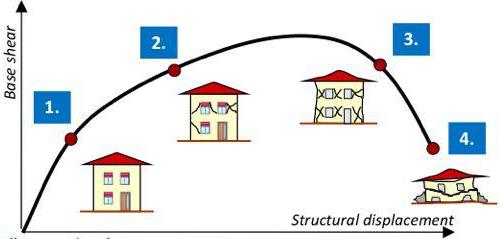
Рисунок 3 – Кривая несущей способности с указанием критериев оценки надежности конструкции:
1 - безопасная непрерывная эксплуатация здания, незначительные повреждения элементов конструкции; 2 - большинство процессов в здании могут быть продолжены, конструкции безопасны для эксплуатации, небольшие повреждения, необходимо восстановление вспомогательных элементов здания; 3 - значительные повреждения, но конструкция остается надежной, при землетрясении возможна безопасная эвакуация из здания, восстановление возможно, но может быть экономически невыгодно; 4 - критическое состояние, разрушение некоторых элементов, восстановление невозможно.
В данной статье рассмотрена трехмассовая динамическая модель с эластомерными опорами. Предложена методика учета высших форм колебаний при оценке сейсмостойкости системы нелиненйым статическим методом. Выполнены расчеты на сейсмические воздействия уровня МРЗ с использованием прямого динамического метода и мультимодального нелинейного статического метода.
2 Методика учета высших форм колебаний
Для определения отклика системы с учетом влияния высших форм колебаний рассмотрим следующий метод, для чего введем понятие модифицированной системы инерционных сил.
Под модифицированной системой инерционных сил будем понимать систему сил, полученную по методу «Корень Квадратный Суммы Квадратов», при которой перемещение верха рассматриваемой расчетной модели будет соответствовать суммарным перемещениям, полученным на основании линейно-спектрального анализа. Графическое представление сложения инерционных сил выполнено на рисунке 4.

Рисунок 4 – Графическое представление метода суммирования модальных откликов «Корень Квадратный Суммы Квадратов»
Согласно [5] для разрушения материала, независимо от того, какая будет приложена нагрузка (т.е. статическое медленное загружение, динамическое – быстрое загружение, однократное или многократное), необходимо затратить одно и то же количество энергии. Таким образом, энергия деформации линейной системы с модифицированной системой инерционных сил тождественна энегрии деформации системы с учетом пластических деформаций (рисцнок 5). Целевое значение энергоёмкости системы возможно определить на основании модифицированной системы инерционных сил:
Wy = Vb·Δ / 2
где Vb - сдвигающая сила в основании системы;
Δ - перемещение верха системы.
Следующим этапом оценки сейсмостойкости является построение на основании нелинейного статического расчета системы с одной степенью свободы при действии модифицированной системы инерционных сил графика зависимости «Усилие в основании
В зависимости от положения характеристической точки на кривой несущей способности возможно оценить общий характер повреждения конструкции в целом (рисунок 3).
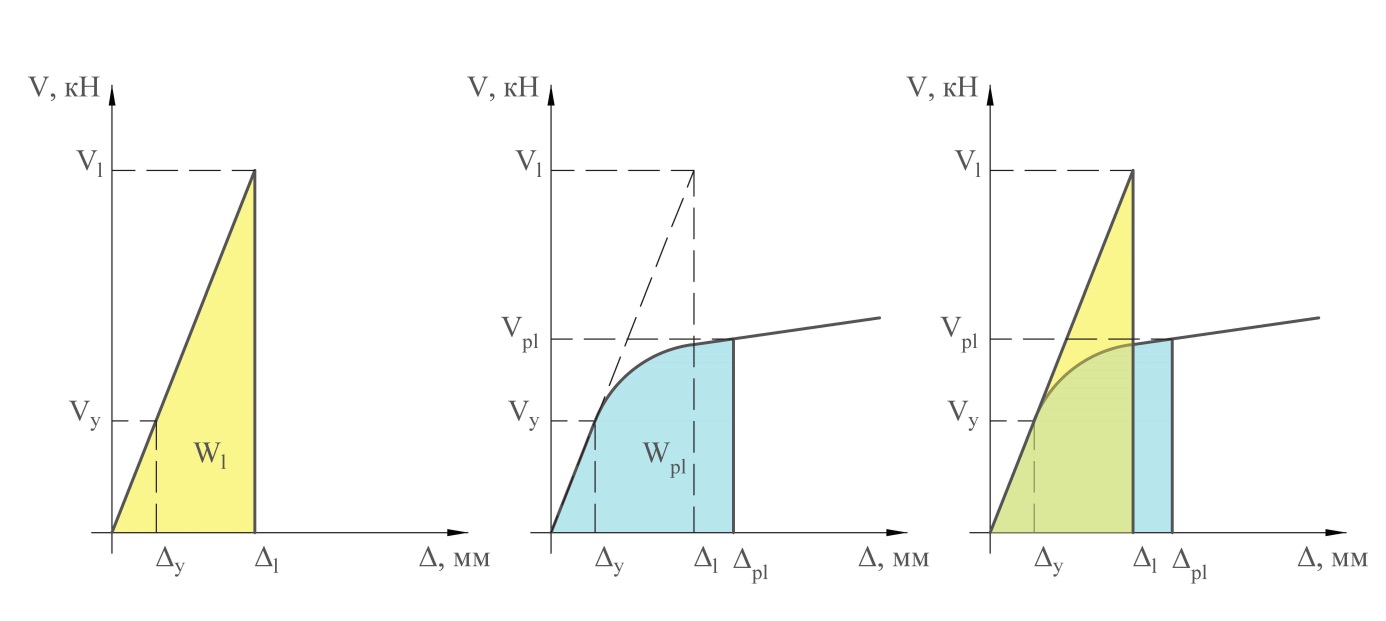
Рисунок 5 – Энергоемкость системы при упругом и упругопластическом поведении системы:
а) упругая работа; б) упругопластическая работа; в) равенство энергий при упругой и упругопластической работе
3 Постановка задачи и апробация методики
В качестве расчетной динамической модели принят вертикальный стержень с тремя равномерно распределенными по высоте сосредоточенными массами. Для каждой из акселерограмм подобрано значение сосредоточенной массы так, чтобы отклик системы на сейсмическое воздействие происходил в заупругой стадии. В основании системы замоделирована эластомерная линейная опора (рисунок 6).
В качестве материала конструкций принята сталь, диаграмма деформирования которой представлена на рисунке 7. Для описания нелинейной работы элементов системы принята модель изотропного упрочнения материала (Bilinear Kinematic Hardening). Диаграммы деформирования стали при растяжении и сжатии принимают одинаковыми с учетом нормируемых сопротивлений стали растяжению и сжатию. Поверхность текучести описывается критерием Вон-Мизеса и представляет из себя цилиндр, ось которого совпадает с осью гидростатического сжатия в осях главных напряжений (рисунок 8).
Параметры демпфирования определены для диапазона частот собственных колебаний, соответствующих первым формам собственных колебаний.
Жесткостные и частотные характеристики систем приведены в Таблице 1.
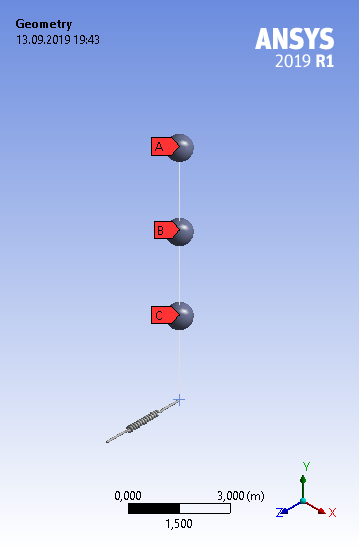
Рисунок 6 – Общий вид расчетной динамической модели
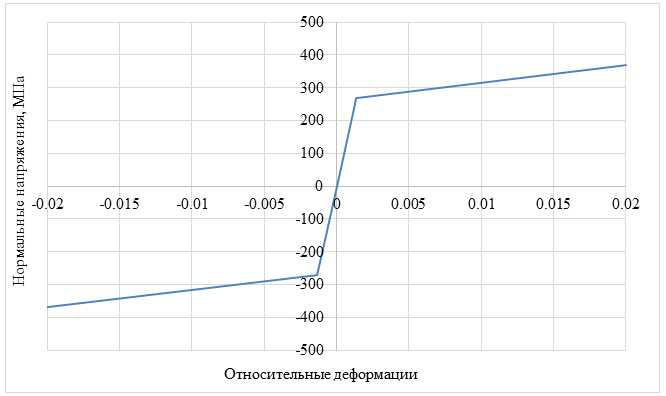
Рисунок 7 – Диаграмма деформирования стали
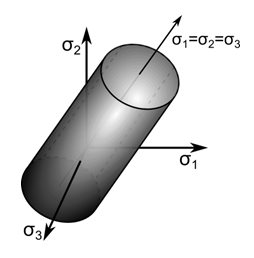
Рисунок 8 – Поверхность текучести по критерию Вон-Мизеса в осях главных напряжений
Сейсмические воздействия заданы следующими однокомпонентными акселерограммами, действующими в плоскости YoZ:
1. Iran, 1978 г. (Erthq. 1);
2. El Centro, USA (California), 1979 г. (Erthq. 2);
3. Duzce, Turkey, 1999 г. (Erthq. 3).
Записи акселерограмм взяты из базы данных PEER Ground Motion Data Base [12].
Таблица 1 – Общие характеристики системы

Для вычисления системы сил при выполнении анализа сейсмостойкости системы мультимодальным нелиненйым статическим методом исходными данными являются инерционные силы первых трех форм колебаний. Характеристики системы приняты в соответствии с таблицей 1.
Распределение инерционных сил и результирующая система сил для сейсмического воздействия Iran, 1978 г. (Erthq1) получены на основании линейно-спектрального анализа.
Для вычисления коэффициента редуцирования инерционных сил выполним статический расчет системы. Полученное значение коэффициента представлено в таблице 2. Также определяется энергоемкость системы.
Следующим этапом оценки сейсмостойкости системы является выполнение нелинейного статического расчета при действии модифицированной системы инерционных сил, на основании которого строится кривая несущей способности в координатах «сдвигающая сила в основании – перемещение верха системы».
Поиск характеристической точки является итерационным: необходимо найти такую точку на графике несущей способности, чтобы площадь образованной под графиком фигуры соответствовала целевой энергоемкости системы.
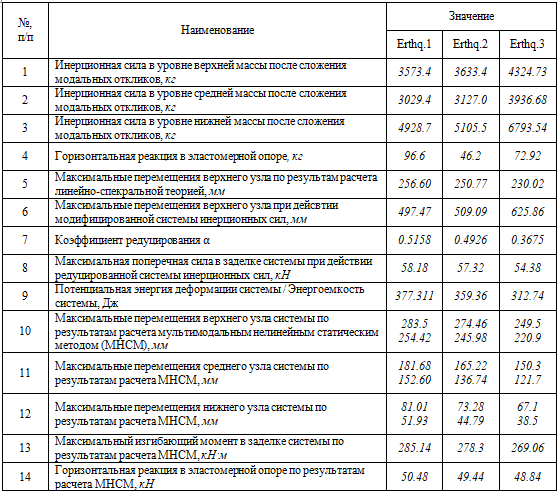
Полученные результаты для сейсмических воздействий Erthq1..3 сведены в таблицу 2.
Отклик системы на сейсмическое воздействие, заданное в виде акселерограмм землетрясений, вычислен в программном комплексе ANSYS R18.2 (Academic version). Расчеты выполнены прямым динамическим методом. Шаг интегрирования
0 < ∆t < 1 / (20f),
где f - рассматриваемая частота системы.
Таким образом, значение
Отклик системы оценивался по следующим параметрам:
- Горизонтальные смещения узлов системы;
- Внутренние усилия в наиболее нагруженных элементах (изгибающий момент, поперечная сила);
- Локализация пластических деформаций.
Результаты расчетов для сейсмических воздействий Erthq.1..3 представлены в сводной таблицах 3-5.
Таблица 2 – Результаты расчета мультимодальным нелинейным статическим методом
3 Результаты
Для оценки погрешности откликов, полученных мультимодальным нелинейным статическим методом, сравним результаты с откликами, полученными на основании прямого динамического метода с использованием записей ускорений Erthq1-3.
Оценка погрешности результатов расчетов представлены в таблицах 3–5.
Для оценки качества полученных данным выполним их статистическую обработку:
- Среднее значение погрешности горизонтальных смещений узлов системы составило 10,52%; среднеквадратичное отклонение – 12,52 %;
- Среднее значения погрешности изгибающих моментов в элементах системы составило 3,59/%; среднеквадратичное отклонение – 3,58 %;
- Среднее значения погрешности поперечных сил в элементах системы составило 12,57%; среднеквадратичное отклонение – 5,18 %.
Таблица 3 – Оценка погрешности мультимодального нелинейного статического метода при сейсмическом воздействии Iran, 1978 г. (Erthq1)
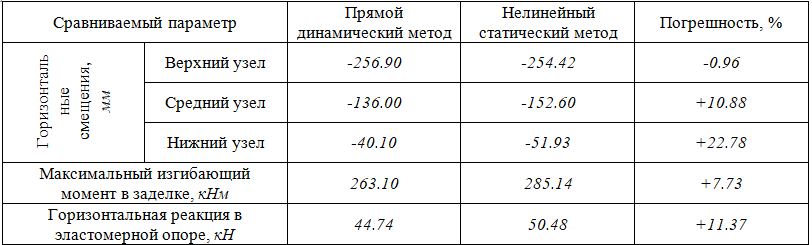
Таблица 4 – Оценка погрешности мультимодального нелинейного статического метода при сейсмическом воздействии El Centro, USA (California) (Erthq2)

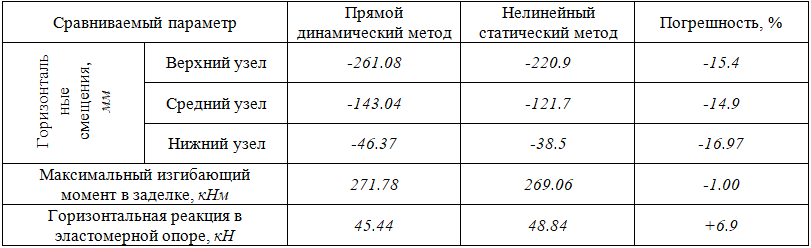
Таблица 5 – Оценка погрешности мультимодального нелинейного статического метода при сейсмическом воздействии Duzce, Turkey, 1999 г. (Erthq3)
Заключение
Для учета влияния высших форм колебаний при оценке сейсмостойкости систем предложена методика поиска начальных инерционных сил для последующего нахождения характеристической точки на графике несущей способности системы – мультимодальный нелиненйый статический метод. По результатам выполненного комплекса расчетов можно сделать вывод о целесообразности применения предложенной методики. Предложенный метод суммирования инерционных сил является наиболее вероятным для определения суммарной инерционной нагрузки. Разница в результатах, полученных прямым динанмическим методом, с результатами на основе мультимодального нелинейного статического метода по всем критериям отклика конструкции не превышает 12.6% и обусловлена вероятным частотным распределением инерционных сил. Введение в теорию нелинейного статического метода понятия «энергоемкость системы» позволяет значительно упростить методику поиска характеристической точки, но основании которой определяется конечное состояние системы после сейсмического воздействия.
Стоит отметить, что при меньших затратах машинного времени мультимодальный нелиненйый статический метод может быть достойной альтернативной прямому динамическому методу.
1. СП 14.13330.2014. Строительство в сейсмических районах.М.:2014
2. Eurocode 8: Seismic Design of Buildings. EUR 25204 EN - 2012
3. Бирбраер А.Н. Расчет конструкций на сейсмостойкость. СПб, 1988
4. О.В. Мкртычев. Безопасность зданий и сооружений при сейсмических и аварийных воздействиях. М.:2010
5. О.В. Мкртычев, Г.А. Джинчвелашвили. Проблемы учета нелинейностей в теории сейсмостойкости (гипотезы и заблуждения). М.:2012
6. Kalkan, E., and Kunnath, S. K. (2004). “Method of modal combinations for pushover analysis of buildings.” Proc. of the 13th World Conference on Earthquake Engineering, August 1-6, 2004, Vancouver, BC, Canada
7. Applied Technology Council (ATC-40). (1996). Seismic evaluation and retrofit of concrete buildings, Redwood, CA
8. FEMA-356. (2000). Prestandard and Commentary for the seismic rehabilitation of buildings, American Society of Civil Engineers (ASCE), Reston, VA
9. Chopra, А. К., & Geol, R. К. ( 1999). Capacity-demand-diagram methods based on inelastic design spectrum. Earthquake Spectra, 637-656
10. Chopra A. (1995). “Dynamics of Structures: Theory and Applications to Earthquake Engineering”, Prentice Hall
11. Chopra A.K., Goel R.K. (2000). ‘Evaluation of NSP to estimate seismic deformation: SDF systems.’ Journal of Structural Engineering, 126(4), 482-490
12. PEER Ground Motion Database // https://ngawest2.berkeley.edu/


















