Ростов-на-Дону, Ростовская область, Россия
Ростов-на-Дону, Ростовская область, Россия
Россия
ГРНТИ 67.23 Архитектурно-строительное проектирование
ГРНТИ 67.01 Общие вопросы строительства
ОКСО 270000 АРХИТЕКТУРА И СТРОИТЕЛЬСТВО
ББК 385 Строительные конструкции
ББК 308 Монтаж, эксплуатация, ремонт машин и промышленного оборудования
ТБК 5414 Строительные конструкции
В статье рассмотрено моделирование ветрового воздействия на здание сложной параметрической формы. Разработано несколько вариантов конечно-элементных моделей – балочные и безбалочные плиты перекрытия с консольными свесами, несущие элементы в виде колонн и пилонов. По результатам динамического расчета выбрано оптимальное конструктивное решение каркаса здания. Моделирование ветрового воздействия выполнено по нормативной документации и в ПК «ANSYS». Анализ результатов счета показал, что напряженно-деформированное состояние элементов каркаса во второй модели отличается от значений полученных по нормативным рекомендациям. Показано, что существующие нормы проектирования требуют уточнения методики определения ветровой нагрузки для зданий и сооружений сложной геометрической формы.
ветровое воздействие, параметрическая архитектура, конструктивные решения, метод конечных элементов, конечно-элементная модель, напряженно-деформированное состояние
Ветровое воздействие вносит большой вклад в напряженно-деформированное состояние конструкций зданий параметрической архитектуры и требует более детального учета ветровой нагрузки , чем в нормативных документах [1].
С целью снижения ветровых воздействий на поверхности здания необходимо выбрать оптимальную конструктивную модель, отвечающую требованиям по несущей способности и соответствующую параметрической форме объекта [2].
Для исследования ветрового воздействия выбрано проектируемое двадцатиэтажное здание параметрической архитектуры административного назначения в г. Ростове-на-Дону.
Численный эксперимент по регулированию напряженно-деформированного состояния плит перекрытий каркаса здания с консольными свесами позволил определить изгибающие моменты, возникающие в зонах пересечения консольного вылета плиты перекрытия и вертикальных несущих элементов, которые необходимо учитывать при конструировании данного узла.
Разработано два варианта конструктивного решения плиты перекрытия - безбалочное (рис. 1а) и с балками (рис. 1б).

Рис.1. Конструктивное решение плиты: а) без балок; б) с балками
При моделировании эксцентриситета стержни сшиваются при помощи абсолютно жестких вставок с узлами конечно-элементной модели плиты. На рис. 2а представлена визуализации балки в виде конечно-элементной сетки. 3D модель фрагмента каркаса здания представлена на рис. 2б.

Рис.2. Визуализация балки: а) КЭ сетка; б) 3D модель
В расчетной модели учтены собственный вес, постоянные и полезные нагрузки. По результатам статического расчета получены перемещения плиты перекрытия, изолинии которых показаны на рис. 3.
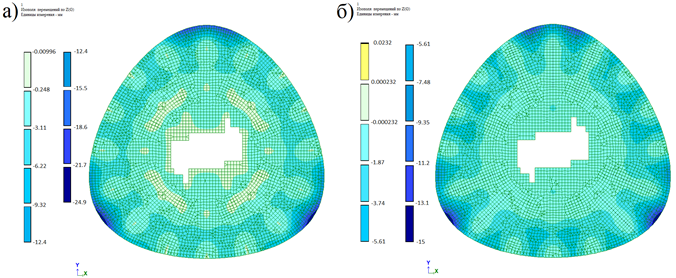
Рис.3. Вертикальные перемещения плиты перекрытия:
а) безбалочной; б) с балками
Максимальные перемещения плиты в первом варианте составляют 24,9 мм, во втором - 15 мм. В качестве ограждающих конструкций предлагается витраж алюминиевый, для которого номеруются значения вертикальных перемещений крайней точки консольного свеса. В связи с этим оптимальной признана вторая конструктивная схема.
Для исследования динамических характеристик разработаны конечно-элементные модели каркаса здания с несущими элементами в виде колон и пилонов в ПК САПФИР и импортированы в ПК ЛИРА САПР [2].
Первая модель: несущие элементы каркаса здания выполнены из бетона класса В25; и включают фундаментную плиту 1500 мм, стены подвала 400 мм, диафрагмы жесткости 250 мм, стены ядра жестокости 300 мм, плиты перекрытия 220 мм, лестничные марши и промежуточные площадки 200 мм, монолитные балки 300х400(h) мм, пилоны в подвале и на 1-4 этажах 1200х500 мм, на 5-7 этажах 1200х400 мм, выше 7 этажа 1200х500 (рис. 4).
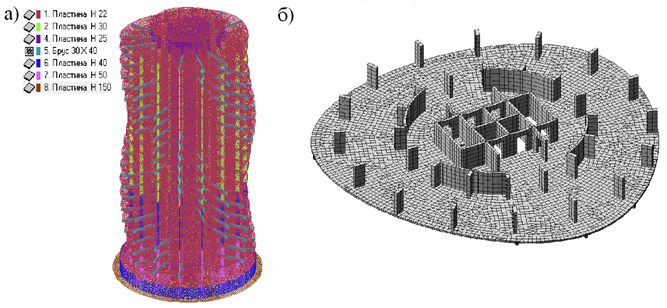
Рис.4. Первая расчетная модель:
а) распределение материалов; б) фрагмент этажа
Вторая модель отличается наличием несущих элементов в виде колонн в подвале и на 1-5 этажах сечением 600х600 мм, в 6-9 этажах – 500х500, выше 9 этажа – 400х400 (рис.5).
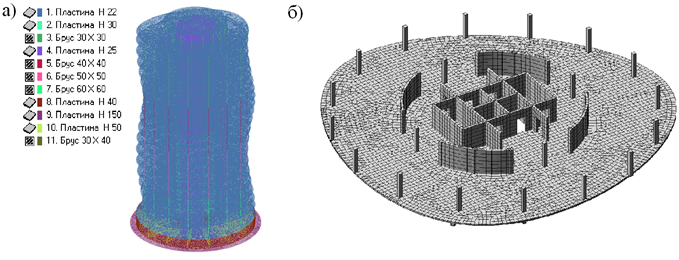
Рис.5. Вторая расчетная модель:
а) распределение материалов; б) фрагмент этажа
В расчетных моделях учтены 8 статических загружений: собственный вес несущих конструкций; постоянные нагрузки; временная (полезная) нагрузка; временная (длительная) нагрузка; постоянная нагрузка от витража и грунта; временная (снеговая) нагрузка; статический ветер по Х; статический ветер по Y.
Для исследования динамических характеристик каркаса здания выполнен модельный анализ, цель которого сводится к определению частот и форм свободных колебаний конечно-элементной модели в заданном диапазоне [3]. Наибольший интерес представляют значения первых (низших) частот свободных колебаний ![]() . Соответствующие формы свободных колебаний дают представление о возможных способах деформирования конструкции. На этапе проектирования модальный анализ оценивает эффективность несущего каркаса сооружения, уточняет принятые значения геометрических и физических констант, выполняет проверку на резонанс [4]. Результаты модального анализа представлены в таблице 1.
. Соответствующие формы свободных колебаний дают представление о возможных способах деформирования конструкции. На этапе проектирования модальный анализ оценивает эффективность несущего каркаса сооружения, уточняет принятые значения геометрических и физических констант, выполняет проверку на резонанс [4]. Результаты модального анализа представлены в таблице 1.
Таблица 1. Частоты и периоды колебаний (сделать на 10)
|
№ формы |
Первый вариант расчетной модели |
Второй вариант расчетной модели |
||||
|
Частота, рад/с |
Частота, Гц |
Периоды, с |
Частота, рад/с |
Частота, Гц |
Периоды, с |
|
|
1 |
3.46 |
0.55 |
1.8155 |
2.78 |
0.44 |
2.2558 |
|
2 |
3.53 |
0.56 |
1.7814 |
3.11 |
0.50 |
2.0192 |
|
3 |
3.82 |
0.61 |
1.6455 |
3.48 |
0.55 |
1.8065 |
|
4 |
11.74 |
1.87 |
0.5350 |
8.41 |
1.34 |
0.7464 |
|
5 |
14.29 |
2.28 |
0.4395 |
12.49 |
1.99 |
0.5027 |
|
6 |
14.90 |
2.37 |
0.4214 |
13.19 |
2.10 |
0.4762 |
|
7 |
23.62 |
3.76 |
0.2659 |
14.75 |
2.35 |
0.4256 |
|
8 |
25.29 |
4.03 |
0.2483 |
21.47 |
3.42 |
0.2924 |
|
9 |
25.85 |
4.12 |
0.2429 |
24.16 |
3.85 |
0.2599 |
|
10 |
25.87 |
4.12 |
0.2427 |
24.53 |
3.91 |
0.2560 |
Первая форма колебаний каркаса здания для двух расчетных моделей приведена на рис. 6.

Рис. 6. Первая форма собственных колебаний каркаса здания:
а) первая расчетная модель; б) вторая расчетная модель
Анализ результатов динамического расчета показал, что первая форма колебаний в первой модели поступательная, во второй - крутильная. Процент вклада модальных масс составил для первой модели 13,4 %, для второй 0%. Характер форм колебаний второй модели показывает недостатки принятых конструктивных решений. Для дальнейших исследований ветрового воздействия принята первая модель с простыми конструктивными решениями по каркасу здания [5].
При расчете пульсационной составляющей ветровой нагрузки необходимо учесть первые 3 формы колебаний, значения частот которых меньше предельных ![]()
Расчет пульсационной нагрузки выполнен по двум методам: на основе нормативных значений, указанных в СП «Нагрузки и воздействия» и при учете действительных значений, полученных по результатам расчета в ПК «ANSYS» [6].
В результате расчета с учетом пульсации ветра, рассчитанной по первому методу, получены перемещения несущих конструкций каркаса здания (рис. 7). Максимальные горизонтальные перемещения составляют вдоль оси X 19,1 мм; вдоль оси Y 20,1 мм, что меньше нормативных значений.

Рис. 7. Перемещения от нормативной ветровой нагрузки:
а) вдоль оси Y; б) вдоль оси X
Выполнено моделирование ветрового воздействия в ПК «ANSYS» для уточнения ветрового давления и зон комфортности здания параметрической формой.
Максимальные горизонтальные перемещения составляют вдоль оси X 30,7 мм; вдоль оси Y 33,1 мм, что меньше нормативных значений (рис.8.).
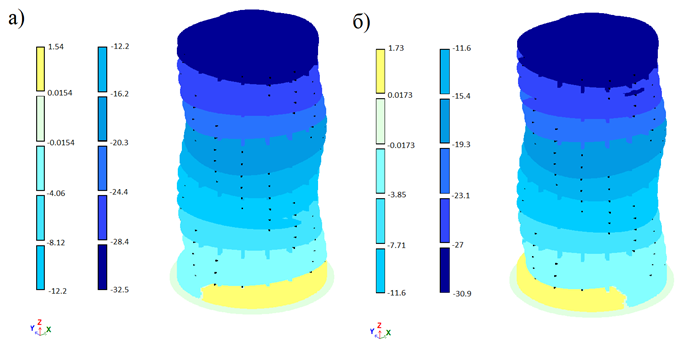
Рис. 8. Перемещения от расчетной ветровой нагрузки:
а) вдоль оси Y; б) вдоль оси X
Моделирование ветровых потоков в ПК ANSYS Fluent позволило уточнить значения нагрузки в расчетной модели каркаса здания параметрической архитектуры. Горизонтальные перемещения увеличились на 40 % по сравнению с результатами, полученными в соответствии с нормативной документацией [7].
Анализ моделирования ветрового воздействия методом конечных элементов показал, что существующие нормы проектирования требуют уточнения методики определения ветровой нагрузки для зданий и сооружений сложной геометрической формы.
При расчете ветровой нагрузки в соответствие с СП ограничены поверхности проектируемых зданий. Объекты параметрической архитектуры сложной геометрической формы действующими нормами не рассматриваются.
Разработан следующий алгоритм расчета объекта параметрической архитектуры на ветровое воздействие:
- регулирование напряженно-деформируемого состояния элементов каркаса зданий и сооружений методом варьирования жесткостей;
- анализ динамических характеристик объекта и выбор рационального - варианта конструктивного решения каркаса здания;
- моделирование ветрового воздействия в ПК ANSYS;
- расчет пульсационной составляющей ветровой нагрузки и определение зон комфортности;
- определение напряженно-деформируемого состояния элементов каркаса здания параметрической архитектуры с учетом пульсационной составляющей ветровой нагрузки.
Предлагаемый авторами подход к расчету ветрового воздействия на объекты параметрической архитектуры позволяет проектировать оптимальные конструкции с достаточной надежностью и долговечностью.
1. Агаханов Э. К., Кравченко Г. М., Осадчий Е.В., Труфанова Е.В. Расчет зданий сложной геометрической формы на ветровые воздействия. Вестник Дагестанского государственного технического университета. Технические науки. - 2017. - № 2. - c. 8-17.
2. Агаханов Э.К. О развитии комплексных методов решения задач механики деформируемого твердого тела. Вестник Дагестанского государственного технического университета. Технические науки. - 2013. - № 2. - c. 39-45.
3. Рабинович И.М. Основы динамического расчета сооружений на действие мгновенных или кратковременных сил, М.- Л., 1945. c. 17-19.
4. Зотова Е.В., Панасюк Л.Н. Численное моделирование динамических систем с большим числом степеней свободы на импульсные воздействия // Инженерный вестник Дона, 2012. № 3 URL: ivdon.ru/magazine/archive/n3y2012/933.
5. Агаханов Э.К., Кравченко Г.М., Труфанова Е.В. Регулирование параметров собственных колебаний пространственного каркаса здания // Вестник Дагестанского государственного технического университета. Технические науки, - 2016. - № 3. - С. 8-15.
6. Гайджуров П.П. Методы, алгоритмы и программы расчета стержневых систем на устойчивость и колебания. Учебное пособие. − Новочеркасск: ЮРГТУ, 2010. 230 с.
7. Зырянов В.В. Методы оценки адекватности результатов моделирования // Инженерный вестник Дона, 2013. № 2 URL: ivdon.ru/magazine/archive/n2y2013/1707.


















