сотрудник с 01.02.2014 по настоящее время
Государственное бюджетное профессиональное образовательное учреждение города Москвы "Политехнический колледж им. Н.Н. Годовикова" (Кафедра Автоматизации, Преподаватель)
сотрудник с 08.09.2017 по настоящее время
Московский технологический университет (Кафедра Метрологии и стандартизации)
аспирант с 01.10.2016 по настоящее время
Московский государственный технический университет имени Н.Э. Баумана (ИУ-1 "Системы автоматического управления")
студент с 01.09.2010 по 31.08.2016
Реутов, г. Москва и Московская область, Россия
ГРНТИ 82.01 Общие вопросы организации и управления
ОКСО 27.06.01 Управление в технических системах
Работа посвящена изучению технологического процесса на предприятиях, занимающихся разработкой оборудования для АЭС с целью выявления нормы времени сборки каркаса. В статье проводится детальный обзор компонентов, входящих в базу шкафов. Проводится выведение в первом приближении уравнения сборки каркаса, как в развернутом, так и в компактном вариантах. По получившемуся уравнению создана математическая модель в среде Matlab Simulink.
норма времени, сборка каркаса, математическая модель, АЭС.
Введение
О проблемах медленного производства оборудования для атомных электростанций мало говорят в современном обществе, поскольку зачастую это закрытая область исследования. Однако она не лишена тех недостатков, о которых упоминают в [1] и для которых разрабатывается «Стратегия тяжелого машиностроения» [2]. В статье [3] был проведен анализ организационных структур с целью их применения на предприятиях подобного типа, но для большего понимания функционирования таких заводских комплексов, стоит рассмотреть составные части технологического процесса и представить пути модификации и стандартизации. В данной статье будет рассматриваться попытка моделирования каркаса – основы.
Создание математической модели сборки каркаса в первом приближении
Как и любой объект управления, в нашем случае сборки, система рассматривается на основе массивов входных и возмущающих параметров. Это необходимо для создания схемы уравнения типа «Вход-Выход». Наиболее подробно данная система описана в [4, с. 12–15],
[5, c. 41–46].
Рассмотрим элементы входного параметра «Y».
В процесс сборки каркаса рассматриваемого оборудования для АЭС входят:
- Каркас – основа, поставляемая производителем «A».
- Детали, изготавливаемые на предприятии «B».
- Особо сложные – на изготовление таких изделий потребуется много времени из-за использования высокосложных станков на подготовительных операциях и / или использование дополнительных модификаций материала, например, закалки Д16 до Д16Т с дальнейшими механическими видоизменениями заготовки, такими как создания радиуса изгиба, фигурного вида изделия и пр. «B1».
- Сложные изделия – изготовление требует использование высокотехнологичных станков «B2».
- Среднесложные детали – изготовление проходит в несколько технологических этапов, например, кроме сверления необходимо нарезать резьбу «B3».
- Простые в изготовлении детали (присущи однотипные операции, например, сверление отверстий в листе АМг6) «B4».
- Доработанные сборочные единицы / детали «C»:
- Сложная доработка (вследствие требования точности позиционирования и т.п. требуется использование сложных станков, например, ЧПУ, фрезерного станка и т.д. Как правило, проходит без участия сборщика) «C1».
- Средняя доработка (например, использование сверлильного станка сборщиком, не требующая высокой точности или уже по намеченные отверстиям) «C2».
- Легкая доработка (зачастую происходит сборщиком, например, процесс распила DIN-рейки с дальнейшей ее обработкой антикоррозионным составом) «C3».
- Детали, снимаемые с каркаса «D».
- Дорабатываемые детали каркаса «E».
- Сборочные единицы / детали, купленные у предприятия – изготовителя «F».
- Крепежный материал «G».
- Самонарезающиеся винты «G1».
- Винты / болты с различными шайбами и гайками «G2».
- Шпильки с различными шайбами и гайками «G3».
- Стойки «G4».
- Стойки с внутренними резьбами «G41».
- Стойки с наружными резьбами «G42».
- Стойки с внутренними и наружными резьбами «G43».
Рассмотрим элементы возмущающего параметра «R»:
- Выполнение другой, более важной на данный момент работы «H».
- Потребности человека (физиологические, психологические) «I».
- Ошибки «J».
- Неверно прикреплена деталь «J1».
- Простой из-за недодачи / неверных устанавливаемых компонентов «J2».
- Потеря крепежного материала «J3».
- Прочее «J4».
- Видоизменение чертежа на стадии сборки «K».
- Усталость рабочего «L».
- Прочее «M».
Выходным параметром будет являться готовое изделие «X».
Покажем на рис. 1 систему сборки каркаса.
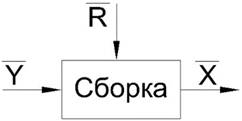
Рис. 1. Сборка каркаса
Составим параметрические уравнения:
Вывод уравнения сборки каркаса оборудования для АЭС
Перед выводом уравнения надо учесть взаимосвязь входных параметров:
- Усталость «L» нарастает постепенно, поэтому необходимо ее учитывать в уравнении при каждом действии.
- Для реализации суммирования времени необходимо делать проход по каждому элементу. Для этого введем счетчики.
В первом приближении уравнение будет иметь следующие допущения:
- Работа происходит от начала до конца.
- Между операциями существует перерыв, в результате которого при переходе на следующую операцию усталость обнуляется.
- Рабочий день бесконечен.
- Видоизменения чертежа не происходит.
- Рабочий не делает никаких дополнительных операций по обработке выданных ему изделий.
С учетом допущений конечное уравнение примет следующий вид:
где:
Видно, что уравнение состоит из двух разных «подобных» частей. Отдельно для входного параметра «Y» и «R».
Стоит пояснить структуру уравнения. Необходимо отметить, что все параметры вводятся в модель предварительно статистически посчитанные для каждого процесса.
Возьмем 2 составные:
- Уравнение параметров «Y» на примере работы с каркасом:
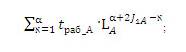
задает цикл суммирования уравнения от 1 до α, α – как описано выше количество операций над каркасом;tраб_А – время работы одной операции над каркасом;
LA – усталость от одной операции над каркасом;
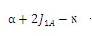– уравнение – счетчик, J1А выполняется два раза, поскольку сначала необходимо снять, а потом переставить на другое место (в частном случае открутить / закрепить) - Уравнение параметров «R» на примере задержки в связи с потребностями человека:
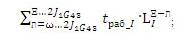
Поскольку в таких процессах ошибок быть не может, уравнение отличается от предыдущего отсутствием 2J1
Модификация уравнения
Вследствие того, что уравнение в чистом виде весьма громоздкое, есть необходимость в его «сворачивании».
Для решения этой задачи необходимо ввести цикл суммирования.
Принимая во внимание тот факт, что в реальных условиях перерывов между процессами практически не бывает, стоит учесть накопление усталости. Для этого будет использоваться цикл произведения.
В результате получим следующее уравнение:
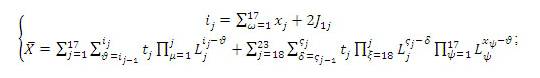
где:xj – количество операций работы с элементом из массива «Y»,J1j – количество ошибок, возникающих при работе с элементом массива «Y»,
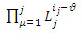– учет накопления усталости при операции с элементом из массива «Y»,
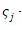– количество операций работы с элементом из массива «R»,
– учет накопления усталости при операции с элементом из массива «R»,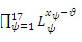 
– учет накопленной усталости после завершения массива «Y». -
Моделирование
Считать для каждого отдельного устройства стандартными математическими методами весьма проблематично из-за необходимости многократной проверки входных составляющих, особенно начиная с 10 операции, вследствие высокой вероятности расчетной ошибки. Для решения этой проблемы целесообразно создать программную модель. Наиболее современными средствами моделирования являются Matlab компании The Mathworks и Mathematica компании Wolfram Research. Воспользуемся первой программой, а точнее ее подблоком Simulink.
В результате подстановки уравнения получим вид модели, показанный на рис. 2–10.
Рис. 2. Уровень запуска модели
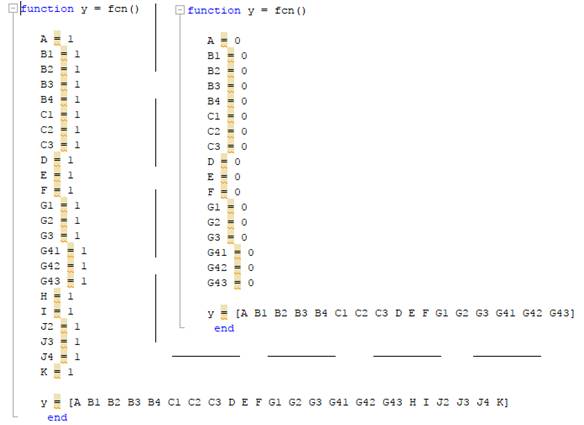
Рис. 3. Уровень ввода данных модели (ввод операционного времени, количества повторений, усталости – слева; ввод количества ошибок – справа)
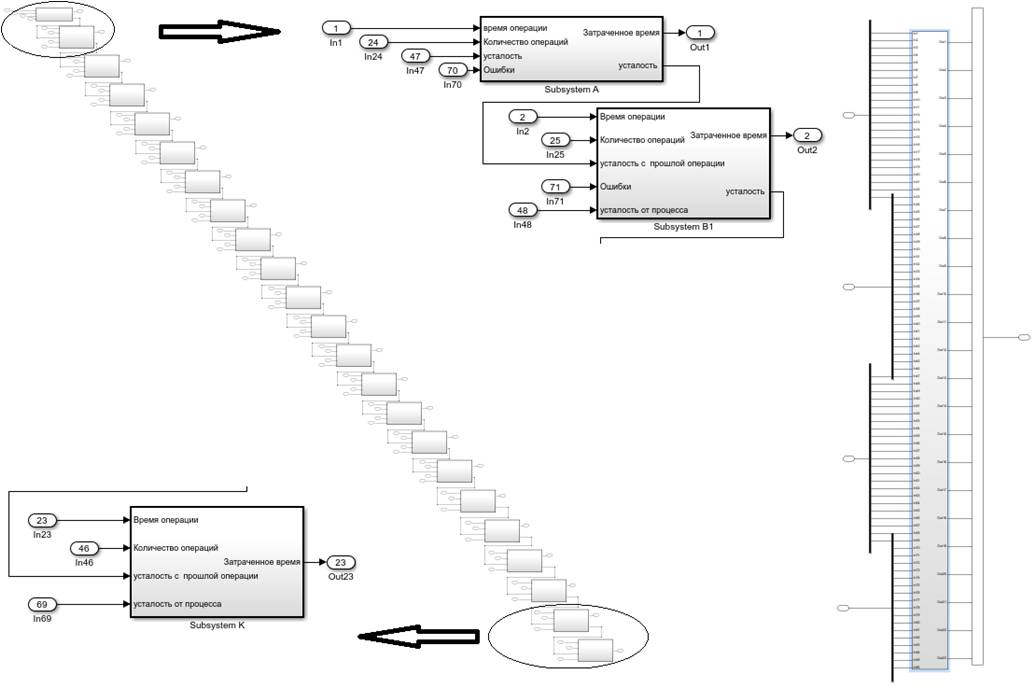
Рис. 4. Расчетный блок – слева, уровень разветвления входных данных – справа
Рис. 5. Блок подсистемы А
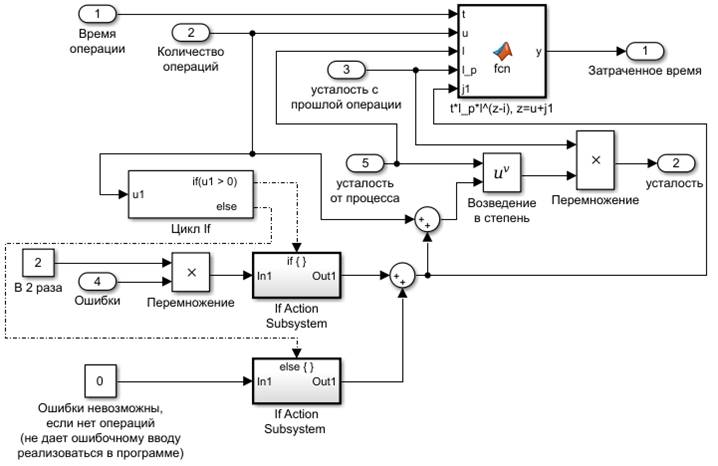
Рис. 6. Блок подсистемы В1…G43
Рис. 7. Блок подсистемы H…J4, M
Рис. 8. Код блока подсистемы A
Рис. 9. Код блока подсистемы B1…G43
Рис. 10. Код блока подсистемы H…J4, M
В связи с возможностью неверного ввода данных, например, ввода ошибок при отсутствии основных операций, была введена дополнительная функция, показанная на рис.5, 6 (блоки – «Цикл If» и «Ifactionsubsystem»).
Заключение
Проведя исследования разработки каркаса силового, управляющего, в частности радиоэлектронного шкафов, было выведено уравнение в первом приближении с рядом допущений. Однако решение столь большого уравнения вызывало бы сложность у специалиста по Нормоконтролю. Для этого была создана математическая модель процесса в среде Matlab Simulink. Проверки более 100 различных подстановок значений входных переменных проводились с использованием сервиса http://www.wolframalpha.com/. Ответы из модели и онлайн калькулятора сходились, в связи с чем можно констатировать, что модель полностью выполняет свои функции.
В дальнейшей работе планируется убрать введенные допущения и модифицировать как уравнение, так и математическую модель.
1. Заболотный Е.А., Бакулина А.А. Состояние отрасли тяжелого машиностроения в России и перспективы ее развития // Проблемы современной науки и образования. - 2017. - № 19, М., С. 62-66.
2. Стратегия развития тяжелого машиностроения на период до 2020 годаи на перспективу до 2030 года, М., 2016г., 82с.
3. Лоскутов И.А. Организационные структуры управления на предприятиях, занимающихся разработкой оборудования для АЭС // Журнал исследований по управлению. Общество с ограниченной ответственностью «Научно-издательский центр ИНФРА-М». - 2018. - Т. 4. - №.4. - С. 40-46. URL: https://naukaru.ru/ru/nauka/article/20745/view (дата обращения: 07.05.2018).
4. Дядик В.Ф., Байдали С.А., Криницын Н.С. Теория автоматического управления. Томский политехнический университет, 2011, Томск, 197 с.
5. Солодовников В.В., Плотников В.Н., Яковлев А.В. Теория автоматического управления техническими системами - МГТУ им. Н.Э. Баумана, 1993, М. - 493 с.
