В работе рассмотрены особенности применения самодиагностики как эффективного средства включения студентов в учебную деятельность на занятиях по математике. Приведены примеры практических задач, в которых используются элементы самодиагностики, несущих в себе элементы интерактивности и убедительной силы в необходимости использования математики. Включение элементов самодиагностики в учебную деятельность дополняет методический арсенал преподавателя вуза при подготовке студентов – будущих психологов в контексте будущей профессиональной деятельности.
самодиагностика, решение задач, математика, студенты, психологи, практические занятия.
Введение
Идея об усилении прикладной направленности в преподавании математики не нова, однако она не потеряла своей актуальности и по сей день. Прикладная направленность обучения математике - это ориентация содержания и методов обучения на применение математики в смежных науках, профессиональной деятельности, народном хозяйстве и быту [1, с. 27].
Большое значение в процессе преподавания математики имеет понимание студентами практической значимости того или иного учебного материала, ближней и дальней перспектив его использования. Движение от ближней - личностно-значимой к практико-прикладной, и далее к квази-профессиональной, исследовательской, творческой и будущей профессиональной деятельности.
Первичный, личностно-значимый материал должен способствовать появлению мотивации к изучению нового материала, обладать высокой убедительной силой в необходимости применять математические методы и модели «здесь и сейчас», в конкретных ситуациях реальной окружающей действительности. Проводимые практические занятия по математике и статистике со студентами - будущими психологами с элементами самодиагностики показали свою эффективность при изучении ряда тем: средние величины, дисперсия, корреляция, регрессия, факторный анализ, многомерное шкалирование, моделирование структурными уравнениями [2, 3]. Проведение этих занятий с элементами самодиагностики должно осуществляться: а) при организации процесса обучения в контексте будущей профессиональной деятельности; б) при широком практическом применении современных информационных технологий и программного обеспечения.
Цель статьи: показать особенности применения самодиагностики как эффективного средства включения студентов в учебную деятельность на занятиях по математике.
Основная часть
Термин «самодиагностика» отсутствует в научной литературе, но близок к понятиям самоизмерения, самоисследования, самоизучения, а в более широком смысле - к самопознанию, рефлексии как самоосознанию, познанию себя. В.Г. Маралов под самопознанием понимает «процесс познания себя, своих потенциальных и актуальных свойств, личностных, интеллектуальных особенностей, черт характера, своих отношений с другими людьми и т.п.» [4, с. 5]. Под самодиагностикой мы понимаем практический прием, способствующий мотивации к изучению нового материала студентами, включения в учебную деятельность.
Рассмотрим более подробно понятие самодиагностики в отношении экспериментальных данных, которые обрабатывают студенты при решении профессионально-ориентированных задач на практических занятиях по математике, информатике, в частности, по математической статистике. Они пользуются сконструированными или реальными данными (которые были кем-то когда-то получены) из учебника, от преподавателя, либо из других источников. На наш взгляд, этого недостаточно, и за основу обрабатываемых данных можно взять материал, который студенты получают самостоятельно в процессе занятий совместно с учебными средствами, интернет-ресурсами [5, 6] и т.д.
Здесь можно выделить несколько вариантов получения данных:
- самодиагностика и самостоятельная обработка полученных данных;
- самодиагностика и обработка полученных данных в парах;
- самодиагностика и обработка данных группой.
Приведем примеры практических задач, в которых используются элементы самодиагностики. Все занятия проводились со студентами-психологами по курсу «Математические методы в психологии» Воронежского государственного педагогического университета.
1. Практическая работа по теме «Коэффициент корреляции r-Спирмена», или «Изучение самооценки при помощи методики ранжирования» [4, с. 121, 122].
Характеристика занятия:
- уровень предметной подготовки: низкий, средний;
- уровень проблемности: репродуктивная деятельность направлена преимущественно на первичное знакомство с материалом;
- тип практического занятия: практикум с элементами самодиагностики;
- форма проведения: индивидуальная [3].
Ход работы:
Цель упражнения: научить определять, в какой степени совпадают оценки «Я-реальное» и «Я-идеальное» с помощью коэффициента корреляции r-Cпирмена.
Инструкция от преподавателя:
- Внимательно прочтите набор из 20 качеств личности: аккуратность, доброта, жизнерадостность, настойчивость, ум, правдивость, принципиальность, самостоятельность, скромность, общительность, гордость, добросовестность, равнодушие, лень, зазнайство, трусость, жадность, подозрительность, эгоизм, нахальство.
- В первый столбик «идеал» под рангом (номером) 1 запишите качество из указанных, которое вы больше всего цените в людях, под рангом 2 - качество, которое цените чуть меньше, и т.д. в порядке убывания значимости. Под рангом 13 укажите то качество - недостаток, который вы легче всего могли бы простить людям (как известно, идеальных людей не бывает, у каждого есть недостатки, но какие-то вы можете простить, а какие-то - нет); под рангом 14 - тот недостаток, который простить труднее, и т.д., под рангом 20 - самое отвратительное с вашей точки зрения качество людей.
- Во второй столбик Я под рангом 1 запишите то качество (из указанных), которое лично у вас сильнее всего развито (независимо от того, достоинство это или недостаток), под рангом 2 - качество, которое развито у вас чуть меньше, и т.д. в убывающем порядке; последние ранги отводятся тем качествам, которые у вас менее всего развиты или отсутствуют.
Обработка результатов:
- Подсчитываем по формуле D = (R1 - R2), где R1 - ранг (номер) 1-го качества в 1-м столбике; R2 - ранг 1-го качества во 2-м столбике; D - разность рангов 1-го качества в столбиках.
Возводим D в квадрат. Посчитаем все D, возведенные в квадрат, их должно быть 20. Предположим, что первое слово в столбике 1 - «ум» (R1 = 1), а в столбике 2 это слово находится на пятом месте, т.е. R2 = 5, тогда по формуле вычисляем (1 - 5) = - 4, возводим в квадрат, получается 16, и т.д. для всех n слов по порядку (n - количество анализируемых качеств, n = 20). - Затем полученные D2 складываем, умножаем на 6, делим произведение на (n • n • n • … • n - n) = (20 • 20 • 20 • … • 20 - 20) = 7980 и, наконец, от 1 отнимаем частное, т.е. находим коэффициент ранговой корреляции: r = (1 - 6 • Σ D) / (n • n • n - n).
- Полученный коэффициент ранговой корреляции сравниваем с психодиагностической шкалой.
2. Практическая работа по теме «Коэффициент корреляции τ-Кендалла», или ролевая игра «Родитель - ребенок».
Характеристика занятия:
- уровень предметной подготовки: низкий, средний;
- уровень проблемности: репродуктивная деятельность направлена преимущественно на первичное знакомство с материалом;
- тип практического занятия: практикум с элементами самодиагностики.
- форма проведения: работа в парах.
Ход работы:
Цель упражнения: научить определять, в какой степени совпадают оценки «родителя» и «ребенка» по отношению к ранжируемым ценностям с помощью коэффициента корреляции τ-Кендалла.
Студенты разбиваются на пары, один студент выступает в роли «родителя», другой - «ребенка».
Преподаватель просит «родителей» и их «детей» проранжировать семь жизненных ценностей, имеющих определяющее значение для личностного благополучия. Дается 5-10 минут. Затем студенты, находящиеся в парах, переписывают друг у друга данные в рангах для представления совместных результатов в два столбца.
На следующем этапе преподаватель просит участников привести таблицу к более удобному виду, в которой ценности «родителя» идут по возрастанию, а ценности его «ребенка» принимают форму, соответствующую его значениям.
Далее составляется графическое представление метода: «Попробуем изобразить данную взаимосвязь в виде двух рядов значений, которые полностью соответствуют друг другу». Далее идет подсчет числа инверсий, и преподаватель показывает студентам, как рассчитывается коэффициент корреляции τ-Кендалла. Все полученные студентами показатели обсуждаются с преподавателем. Обсуждаются другие существующие коэффициенты корреляции, правила их расчета, достоинства, недостатки, ограничения.
3. Практическая работа по теме «Корреляционно-регрессионный анализ», или «Введение в структурное моделирование».
Характеристика занятия:
- уровень предметной подготовки: высокий (знание основ корреляционно-регрессионного анализа, навыки работы в программе Excel или SPSS);
- уровень проблемности: репродуктивная деятельность направлена преимущественно на первичное закрепление нового материала, дальнейшее изучение которого предполагает реконструктивную и творческую, поисковую деятельность;
- тип практического занятия: групповой практикум с элементами самодиагностики.
Приборы и материалы: компьютер с программой SPSS (+AMOS) [10].
Ход работы:
Цель упражнения: закрепить навыки вычисления коэффициентов корреляции, регрессии и приобрести начальный опыт построения структурных схем.
Участникам раздаются бланки методик:
- тест «Исследование тревожности (опросник Спилбергера) [11];
- методика определения стрессоустойчивости и социальной адаптации Холмса и Раге [12].
В процессе раздачи бланков и ознакомления с методиками студенты обсуждают вместе с преподавателем возможные связи между такими категориями, как «стрессоустойчивость» и «тревожность», «личностная тревожность» и «ситуативная тревожность». Так как методика Холмса и Раге основана на подсчете различных событий, случившимися с человеком за последний год, то преподаватель предлагает группе гипотезу о причинно-следственной связи между стрессоустойчивостью и тревожностью: «Чем выше у человека стрессоустойчивость, тем его ниже тревожность, или чем ниже стрессоустойчивость, тем выше тревожность». Далее группе предлагается пройти два предложенных теста и, подсчитав собственные результаты передать преподавателю их для совместного анализа.
Результаты, полученные в группе из N человек, студенты заносят в таблицу.
Анализ результатов:
В результате парной обработки столбцов с помощью коэффициента корреляции Пирсона в программе SPSS студенты получают корреляционную матрицу.
Далее преподаватель вместе с группой проверяют гипотезу о том, что, чем выше степень стресса, которую получил человек за определенный период времени, тем выше его личностная и ситуативная тревожность (см. рис. 1).
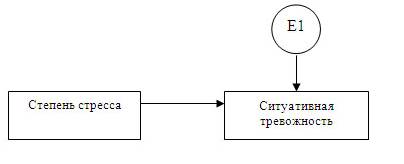
Рис. 1. Влияние стресса на ситуативную тревожность

Рис. 2. Влияние стресса на личностную тревожность
Моделирование начинается с построения графиков в Excel, затем переходим к построению и расчету самых простых регрессий в программе AMOS SPSS (см. рис. 1 и 2). Совместно подтверждается или опровергается выдвинутая гипотеза о влиянии стресса на личностную и ситуативную тревожность.
Заключение
При решении математических задач студенты могут принимать активное участие, т.е. использовать собственные данные, полученные в результате самодиагностики. Самодиагностика выступает здесь как важное средство включения студентов в исследовательскую деятельность и несет элементы интерактивности, убедительной силы в необходимости использования математики, самореализации. Положительным также является то, что в процессе совместной работы со студентами открывается огромный простор для фантазии и творчества преподавателя по разработке интересных и эффективных занятий, организации деятельности учащихся.
Самодиагностика как средство согласуется с требованиями по реализации компетентностного подхода в образовании, где нужно «…предусматривать широкое использование в учебном процессе активных и интерактивных форм проведения занятий (компьютерные симуляции, деловые и ролевые игры, разбор конкретных ситуаций, психологические и иные тренинги)…» [13].
Применение математико-статистических методов и компьютера в процессе обработки данных тесно связано с содержанием профессиональной деятельности будущих психологов: диагностической, коррекционно-развивающей, консультационной, психотерапевтической, исследовательской, административной и т.д. Поэтому особенности будущей профессиональной деятельности этих специалистов должны учитываться в процессе их математической подготовки. Однако ограничиваться на решении практических задач в русле только будущей профессиональной деятельности студентов не следует. Предлагаемые прикладные задачи могут соответствовать деятельности будущего специалиста, а также могут иметь лишь контуры будущей профессиональной деятельности. Применимость математических методов необходимо показывать и в других социогуманитарных направлениях - педагогике, социологии, экономике и т.д.
1. Колягин Ю.М. О прикладной и практической направленности обучения математике [Текст] / Ю.М. Колягин, В.В. Пикан // Математика в школе. - 1985. - № 3. - С. 27-34.
2. Остапенко Р.И. Самодиагностика как условие формирования математической компетентности студентов психологических специальностей [Электронный ресурс] / Р.И. Остапенко // Современные научные исследования и инновации. - 2013. - № 10. - URL: http://web.snauka.ru/issues/2013/10/28172 (дата обращения: 24.07.2015). EDN: https://elibrary.ru/RJEDXN
3. Остапенко Р.И. Формирование информационно-математической компетентности студентов вузов посредством самодиагностики [Текст] / Р.И. Остапенко // Известия Воронежского государственного педагогического университета. - 2014. - № 3 (264). - С. 81-83; Остапенко Р.И. Управление процессом формирования информационно-математической компетентности студентов вузов посредством самодиагностики [Текст] / Р.И. Остапенко // Государственный советник. - 2014. - № 1 (5). - С. 160-164.
4. Маралов В.Г. Основы самопознания и саморазвития [Текст]: учеб. пособие для студ. сред. пед. учеб, заведений / В.Г. Маралов. - 2-е изд., стер. - М.: Академия, 2004. - 256 с. EDN: https://elibrary.ru/QXKLXL
5. Капустин А.Н. Использование Интернет-ресурсов в процессе решения математических задач студентами вузов [Текст] / А.Н. Капустин, Р.И. Остапенко // Современные научные исследования и инновации. - 2014. - № 1 (33). - С. 34. EDN: https://elibrary.ru/RUQDRL
6. Остапенко Р.И. Использование Интернет-ресурсов при решении математических задач студентами вузов спортивной направленности [Текст] / Р.И. Остапенко // Перспективы науки и образования. - 2014. - № 2 (8). - С. 90-94. EDN: https://elibrary.ru/SCAFYF
7. Баданова Т.А. Влияние внешних факторов организации обучения и готовности студентов к групповому взаимодействию при выборе интерактивных методов обучения математическим дисциплинам в вузе [Электронный ресурс] / Т.А. Баданова, А.В. Костенко // Интернет-журнал «НАУКОВЕДЕНИЕ». - 2015. - Том 7. - № 3. - URL: http://naukovedenie.ru/PDF/22PVN315.pdf (дата обращения: 25.06.2015). DOI: http://dx.doi.org/10.15862/22PVN315 EDN: https://elibrary.ru/UMFYDZ
8. Остапенко Р.И. Формирование математической компетентности будущих педагогов-психологов [Текст]: автореф. дис. …канд. пед. наук / Р.И. Остапенко. - Елец, 2009. EDN: https://elibrary.ru/NKVKZZ
9. Остапенко Р.И. Методика преподавания математических дисциплин студентам гуманитарных специальностей в русле компетентностного подхода [Текст] / Р.И. Остапенко // Вестник Воронежского государственного университета. Серия: Проблемы высшего образования. - 2011. - № 2. - С. 70-72. EDN: https://elibrary.ru/ONUVYH
10. Остапенко Р.И. Особенности анализа лонгитюдных данных в психолого-педагогических исследованиях с помощью AMOS SPSS [Текст] / Р.И. Остапенко // Современные научные исследования и инновации. - 2014. - № 4 (36). - С. 74. EDN: https://elibrary.ru/SFCJRN
11. Psylist.net [сайт] / Тест «Исследование тревожности» (опросник Спилбергера) [Электронный ресурс] // URL: http://psylist.net/praktikum/istre.htm (дата обращения: 27.07.2015).
12. Azps.ru [сайт] / Методика определения стрессоустойчивости и социальной адаптации Холмса и Раге [Электронный ресурс] // URL: http://azps.ru/tests/2/tt18.html (дата обращения: 27.07.2015).
13. Федеральный государственный образовательный стандарт высшего профессионального образования по направлению подготовки 030300 «Психология» (Квалификация (Степень) «Бакалавр») (в ред. приказа Минобрнауки России от 31.05.2011 № 1975).






