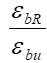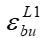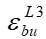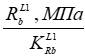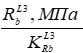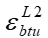from 01.01.2019 until now
Russian Federation
Russian Federation
UDC 69.01
CSCSTI 67.11
Operation is the longest stage of the life cycle of a capital construction facility. At the pre-investment stage, the idea of a capital construction facility is being conceived and worked out, at the investment stage, a project is being developed, the facility is being built, and during the operation of the capital construction facility, it is assumed that the goals and objectives that were set at previous stages will be realized. An important task in this regard is to ensure the uninterrupted operation of the facility for a long time, as well as, as far as possible, prolonging its operation, which is influenced by many factors, one of which is the humidity regime, the influence of which on reinforced concrete structures leads to periods of hardening or the development of destructive processes in concrete, which is important when predicting the service life of structures. In this regard, three variants of the operating conditions of reinforced concrete structures were considered: favorable, normal and unfavorable. A method for calculating the ultimate resistance of concrete during prolonged stretching (Rbt) and compression (Rb), as well as the ultimate relative deformations under short-term axial compression (bR), axial tension (btR), and under the prolonged inhomogeneous compression (b2) and inhomogeneous tension (bt2), adjusted depending on the humidity conditions and the concrete class is proposed. The calculation results are presented.
capital construction facility, life cycle, management, reinforced concrete structures, concrete, humidity regime
Введение
Обеспечение надежности и долговечности несущих железобетонных конструкций каркасного здания непроизводственного назначения является приоритетным направлением при управлении его жизненным циклом. Наиболее стратегически важным компонентом с точки зрения конструктивной безопасности длительно эксплуатируемых зданий является несущая способность основных конструктивных элементов на завершающем этапе их жизненного цикла, то есть в конце заданного срока службы объекта [1, 2]. При этом конструкции должны быть запроектированы таким образом, чтобы их несущая способность не снижалась ниже заданного нормативного предела весь период эксплуатации, вплоть до времени вывода здания из эксплуатации [1-4]. Решение этой задачи при проектировании железобетонных конструкций сильно осложняется в связи с тем, что в нагруженном бетоне, как правило, реализуются одновременно разнонаправленные процессы упрочнения и разупрочнения, которые в процессе длительной эксплуатации зданий и сооружений под действием различных внешних воздействий, в том числе несиловых (отрицательная или положительная температура, влажная или сухая окружающая среда, водные или паровоздушные химические реагенты и др.) могут поочередно как ускоряться, так и замедляться вплоть до их полной остановки [4, 5].
В данной статье представлены результаты, связанные с разработкой методики определения деформативно-прочностных характеристик бетонов, из которых были изготовлены несущие железобетонные конструкции, после их длительной эксплуатации с учетом влажностных условий окружающей среды в составе каркасных зданий непроизводственного назначения.
Методы, оборудование, материалы
Теоретической основой исследования являются научные разработки, материалы научно-практических конференций, база нормативно-правовых документов [3, 6, 7]. В качестве методологического инструментария использована общенаучная методология, которая предусматривает системный, комплексный, факторный и процессный подходы к решению проблем, а также применение таких методов, как анализ и синтез, экспертные оценки.
Основная часть
При изготовлении сборной или монолитной железобетонной конструкции высокая относительная влажность окружающей среды является основополагающим фактором для набора прочности бетона. При недостаточной влажности окружающей среды, например, в летний жаркий период, если не принимается мер по поддержанию высокой влажности бетона, темпы гидратации цемента снижаются, прочность и трещиностойкость изгибаемой железобетонной конструкции могут быть значительно ниже проектных величин. После того, как конструкция была изготовлена и набрала требуемую прочность, процессы, связанные с гидратацией цемента в бетоне, продолжаются, хотя и не так активно, как при изготовлении. С учетом того, что стадия эксплуатации объекта капитального строительства, в целом, и конструкций, входящих в его состав, в частности, рассчитана на длительный период, в течение этого времени тот или иной влажностный режим окружающей среды понемногу способствует проявлению в бетоне дополнительной гидратации цемента или, наоборот, постепенной деактивации химических связей между цементной матрицей и заполнителями. Это так называемые периоды упрочнения и проявления деструктивных процессов в бетоне. В ходе длительной эксплуатации изгибаемых и внецентренно сжатых железобетонных конструкций период развития деструктивных процессов деформативно-прочностных характеристик в бетоне становится преобладающим, а темпы этого процесса во многом зависят от относительной влажности окружающего воздуха.
В зависимости от средней относительной влажности воздуха во внутренних помещениях зданий в СП 63.13330 предлагается учитывать следующие группы условий эксплуатации железобетонных конструкций при продолжительном действии нагрузки:
– благоприятные условия эксплуатации (относительная влажность воздуха более 75%);
– нормальные условия эксплуатации (относительная влажность воздуха находится в диапазоне от 40 до 75%);
– неблагоприятные условия эксплуатации (относительная влажность воздуха менее 40%).
Для каждой из указанных трех групп в СП 63.13330 приведены усредненные значения предельных относительных деформаций при длительном осевом сжатии (eb0) или осевом растяжении (ebt0), а также при длительном неоднородном сжатии (eb2) или неоднородном растяжении (ebt2). Параметры eb2 и ebt2 соответствуют наибольшим величинам относительной деформации в сжатой и растянутой зонах бетона изгибаемого или внецентренно сжатого длительно нагруженного элемента, соответственно, при его разрушении по сжатой зоне или при образовании первой трещины в растянутой зоне [3].
Расчетные сопротивления бетона сжатию Rb приняты в СП 63.13330 без учета влияния относительной влажности воздуха. Конкретные величины Rb находятся путем умножения нормативных сопротивлений бетона Rbn для рассматриваемого класса по прочности на сжатие на коэффициент 0,69, получаемый из отношения γb1/γb. В СП 63.13330 γb1 = 0,9 – коэффициент условий работы бетона в железобетонной конструкции, учитывающий действие на нее только постоянных и длительных нагрузок, а параметр γb = 1,3 является коэффициентом надежности по бетону при сжатии. Аналогичные расчетные характеристики бетона при длительном растяжении Rbt также приняты без учета градации по группам влияния относительной влажности воздуха, а отношение γb1/γb составляет 0,60.
Для выполнения конструктивных расчетов изгибаемых и внецентренно сжатых железобетонных элементов при продолжительном действии на них нагрузки в настоящее время, как правило, привлекаются прикладные программы для ЭВМ. При этом в составе алгоритмов этих программ более целесообразным было бы использовать различные по величине значения предельных относительных деформаций при осевом (eb0) и неоднородном сжатии (eb2), при осевом (ebt0) и неоднородном растяжении (ebt2) в зависимости от классов бетона для трех групп по влажностным условиям. Расчетные сопротивления бетона сжатию Rb и растяжению Rbt также должны учитывать влияние относительной влажности воздуха в помещениях, в частности, применительно к трем группам диапазонов, указанным в таблице 1.
Таблица 1
Относительные деформации бетона при длительном сжатии и растяжении согласно СП 63.13330
|
Относительная влажность воздуха, % |
Относительные деформации тяжелого, мелкозернистого и напрягающего бетона при продолжительном действии нагрузки |
|||
|
при сжатии |
при растяжении |
|||
|
осевом (εb0) |
неоднородном (εb2) |
осевом (εbt0) |
неоднородном (εbt2) |
|
|
> 75 |
0,0030 |
0,0042 |
0,00021 |
0,00027 |
|
40-75 |
0,0034 |
0,0048 |
0,00024 |
0,00031 |
|
< 40 |
0,0040 |
0,0056 |
0,00028 |
0,00036 |
Для разработки методики определения деформативно-прочностных характеристик бетонов для сжатия и растяжения с учетом различных влажностных условий на завершающем этапе эксплуатации зданий непроизводственного назначения принимаем энергетический подход к разрушению бетона, который впервые предложил профессор В.М. Бондаренко [7]. Согласно данному подходу, учет режимности нагружения основан на постулате о сохранении в качестве постоянной величины в течение времени удельной потенциальной энергии деформирования материала к моменту его разрушения:
 (1)
(1)
Энергетический подход к разрушению бетона при сжатии и растяжении в том или ином виде применяли также и другие ученые [4, 8-11]. Чтобы перейти к непосредственному применению постулата В.М. Бондаренко, необходимо определить параметры нелинейных диаграмм эталонного сжатия (рис. 1, поз. 1) и растяжения (рис. 1, поз. 3) бетона заданного класса по прочности на сжатие.

Рис. 1. Диаграммы кратковременного деформирования бетона при центральном и неоднородном сжатии
(поз. 1 и 2) и растяжении (поз. 3 и 4): jb1 = arctg(Eb1); jb2 = arctg(Eb2) [12]
Диаграмма на рис. 1 была ранее представлена в работе [12], только в качестве предельного сопротивления при сжатии и растяжении в данной работе принимаются нормативные параметры Rbn и Rbtn вместо расчетных параметров Rb и Rbt, так как предметом исследования данной работы является, в том числе, уточнение расчетных параметров в зависимости от класса бетона при разных режимах влажностных условий.
Описание диаграммы (рис. 1) можно представить в виде уравнения [1, 4, 12]:
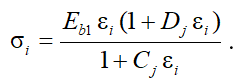 (2)
(2)
Описание параметров функции (2) представлено в работе [12]. Для определения напряжений и деформаций бетона при сжатии параметры указываются с индексом i = b, для определения напряжений и деформаций бетона при растяжении параметры указываются с индексом i = bt. Для нахождения параметров диаграмм центрального сжатия бетона используются как экспериментальные данные [13], так и общепринятые теоретические предпосылки [1, 14].
На основании обобщения данных, представленных в работах [1, 13-15], для определения величин ebR и ebtR применительно к тяжелому бетону классов от B10 до B60 можно рекомендовать следующие эмпирические зависимости:
 (3)
(3)
 (4)
(4)
Значения параметров Eb1 и параметров нелинейности Db1, Cb1 определяем с помощью уравнений (5) - (7) [11]. Начальный модуль упругости бетона при сжатии Eb1 зависит от нормативного модуля Ebn и всегда его превышает. Начальный модуль упругости Eb1 принимается одинаковым как при растяжении, так и при сжатии бетона одного и того же класса. Параметры нелинейности Dbt1 и Cbt1, необходимые для построения кривых, характеризующих центральное растяжение бетона, определяются по зависимостям, аналогичным (6) и (7):
 (5)
(5)
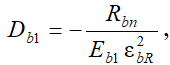 (6)
(6)
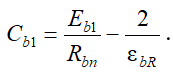 (7)
(7)
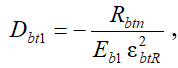 (8)
(8)
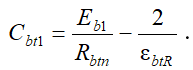 (9)
(9)
Теперь, зная деформативно-прочностные характеристики бетона при центральном (эталонном) сжатии и растяжении, можно определить параметры диаграмм, используемых совместно с гипотезой плоских сечений для системы уравнений, описывающих криволинейные эпюры напряжений в сжатых и растянутых зонах изгибаемых и внецентренно сжатых железобетонных элементов [6, 8, 11, 17, 18]. Эти диаграммы представлены на рис. 1, поз. 2 (неоднородное сжатие) и рис. 1, поз. 4 (неоднородное растяжение).
Для математического представления указанных диаграмм принимается функция, аналогичная (2) с учетом замены индекса 1 при неизвестных параметрах на 2. Так, для нахождения параметров диаграммы при неоднородном сжатии бетона (Eb2, Db2, Cb2) и величины предельной относительной деформации (ebu) при кратковременном нагружении приняты гипотезы и допущения, представленные в работах [11, 19].
Аналитическое отображение принятых гипотез приводит к следующей системе уравнений:
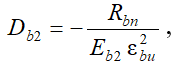 (10)
(10)
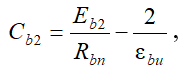 (11)
(11)
 (12)
(12)
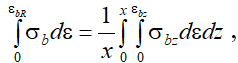 (13)
(13)
где Db2, Cb2 – параметры нелинейности, необходимые для построения кривых, отображающих характер неоднородного сжатия бетона; z – текущее расстояние от нейтральной оси сечения до рассматриваемого волокна эпюры напряжений в сжатой зоне бетона; x – высота сжатой зоны бетона в сечении изгибаемого железобетонного элемента; σbz – текущее напряжение в рассматриваемом волокне эпюры напряжений; εbz – текущая относительная деформация в рассматриваемом волокне эпюры деформаций в сжатой зоне бетона.
Зависимости (12) и (13) после интегрирования будут иметь следующий вид (для сжатой зоны изгибаемого железобетонного элемента):
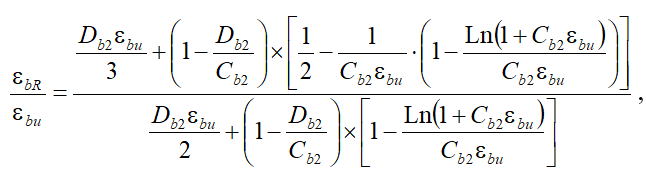 (14)
(14)

 (15)
(15)
Такой же подход используется при нахождении неизвестных параметров (Dbt2, Cbt2) диаграммы при неоднородном растяжении бетона и величины предельной относительной деформации (ebtu) при кратковременном нагружении [12]. Начальный модуль упругости Eb2, найденный из решения системы нелинейных уравнений (10), (11), (14), (15) для неоднородного сжатия бетона, остается таким же для неоднородного растяжения. В связи с принятием указанного условия система разрешающих уравнений базируется не на четырех, а на трех зависимостях с учетом замены переменных, связанных со спецификой неоднородного растяжения [12]:
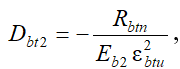 (16)
(16)
 (17)
(17)

 (18)
(18)
Представляется, что аналогичный подход можно применить для определения длительной прочности бетона, находящегося в условиях неоднородного сжатия или растяжения, характеризуемого периодом нагружения образца до разрушения в течение заданного в проекте периода его эксплуатации, равного, например, 75 лет. Следует отметить, что решению указанной проблемы посвящены работы многих известных ученых [2, 7, 9, 20], но в них использовались несколько другие подходы. На рисунке 2 представлены зависимости, показывающие качественный вид диаграмм «напряжения – относительные деформации» для кратковременного неоднородного нагружения (рис. 2, поз. 1), для длительного периода нагружения при благоприятных условиях эксплуатации (рис. 2, поз. 2), то же, при нормальных условиях эксплуатации (рис. 2, поз. 3), а также при неблагоприятных условиях эксплуатации (рис. 2, поз. 4).
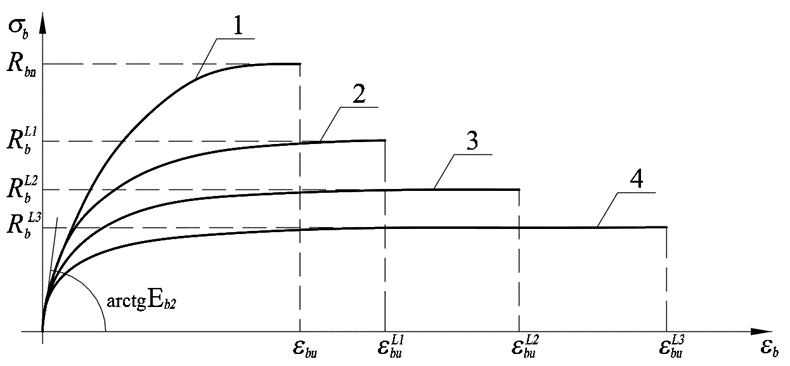
Рис. 2. Диаграммы деформирования бетона при неоднородном кратковременном (1) и длительном сжатии с учетом различных условий эксплуатации: 2 – благоприятные условия;
3 – нормальные условия; 4 – неблагоприятные условия
На рис. 2 и далее в формулах принадлежность какого-либо параметра диаграммы деформирования бетона при неоднородном сжатии к его длительному нагружению обозначается верхним индексом L (например 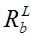 ,
,  ,
,  ).
).
Далее определяем параметры диаграмм длительного неоднородного сжатия бетонов с учетом различных влажностных условий на завершающем этапе эксплуатации зданий непроизводственного назначения с железобетонным каркасом.
Принимаются гипотезы и допущения, описанные в работах [11, 19]. Аналитически данные гипотезы и допущения отображаются в виде системы уравнений:
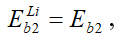 (19)
(19)
 (20)
(20)
 (21)
(21)
 (22)
(22)
где индекс Li обозначает принадлежность параметра к неоднородному длительному сжатию и к одной из трех групп по условиям длительной эксплуатации (i = 1, 2, 3).
Последнее равенство (22) отражает гипотезу об инвариантности величины удельной энергии деформирования бетона при сжатии непосредственно перед его разрушением. В результате его интегрирования и после небольших преобразований получаем следующую зависимость:

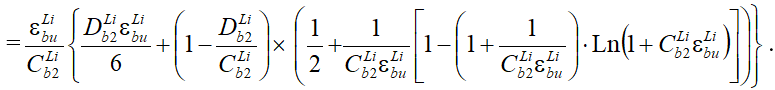 (23)
(23)
Первое из уравнений полученной системы (19) по существу является тождеством, и его можно исключить из рассмотрения. В оставшихся трех уравнениях (20) - (23) неизвестными являются четыре параметра (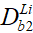 ,
,  ,
,  ,
, 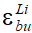 ). В качестве недостающего четвертого уравнения принимаем эмпирическую зависимость для определения величины предельной относительной деформации бетона
). В качестве недостающего четвертого уравнения принимаем эмпирическую зависимость для определения величины предельной относительной деформации бетона  , позволяющую учесть класс тяжелого бетона по прочности на сжатие от B10 до B60, а также принадлежность к одной из трех групп по условиям его длительной эксплуатации. Для построения такой зависимости используем алгебраическое выражение, аналогичное (3), в котором числовые коэффициенты подобраны таким образом, чтобы для каждой группы условий эксплуатации усредненное значение предельной относительной деформации бетона
, позволяющую учесть класс тяжелого бетона по прочности на сжатие от B10 до B60, а также принадлежность к одной из трех групп по условиям его длительной эксплуатации. Для построения такой зависимости используем алгебраическое выражение, аналогичное (3), в котором числовые коэффициенты подобраны таким образом, чтобы для каждой группы условий эксплуатации усредненное значение предельной относительной деформации бетона  соответствовало рекомендациям, приведенным в СП 63.13330:
соответствовало рекомендациям, приведенным в СП 63.13330:
– для благоприятных условий длительной эксплуатации:
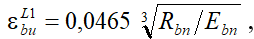 (24)
(24)
– при нормальных условиях эксплуатации:
 (25)
(25)
– для неблагоприятных условий эксплуатации:
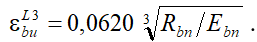 (26)
(26)
Аналогичный прием используется для нахождения неизвестных параметров диаграмм при неоднородном длительном растяжении бетонов ( ,
, ,
, ,
,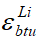 ) с учетом различных влажностных условий на завершающем этапе эксплуатации зданий непроизводственного назначения с железобетонным каркасом. Начальный модуль упругости бетона Eb2 остается неизменным по величине для неоднородного длительного растяжения. Применительно к указанным видам диаграмм деформирования бетонов принимается система уравнений, аналогичных (20) - (23) с учетом изменения обозначений параметров, связанных со спецификой неоднородного растяжения:
) с учетом различных влажностных условий на завершающем этапе эксплуатации зданий непроизводственного назначения с железобетонным каркасом. Начальный модуль упругости бетона Eb2 остается неизменным по величине для неоднородного длительного растяжения. Применительно к указанным видам диаграмм деформирования бетонов принимается система уравнений, аналогичных (20) - (23) с учетом изменения обозначений параметров, связанных со спецификой неоднородного растяжения:
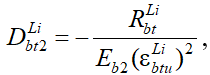 (27)
(27)
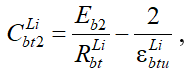 (28)
(28)
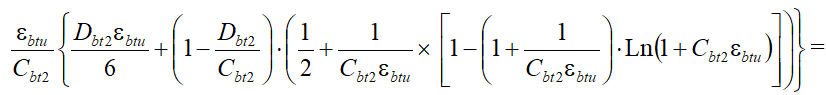
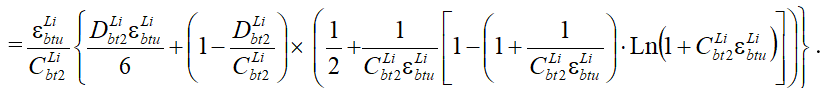 (29)
(29)
Получаем в итоге систему трех уравнений с четырьмя неизвестными параметрами (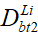 ,
, ,
,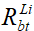 ,
, ), что не позволяет найти их значения. В качестве недостающего четвертого уравнения принимаем эмпирическую зависимость для определения величины предельной относительной деформации бетона
), что не позволяет найти их значения. В качестве недостающего четвертого уравнения принимаем эмпирическую зависимость для определения величины предельной относительной деформации бетона  , позволяющую учесть класс тяжелого бетона по прочности на сжатие от B10 до B60, а также принадлежность к одной из трех групп по условиям его длительной эксплуатации. Для построения такой зависимости используем алгебраическое выражение, аналогичное (4), в котором числовые коэффициенты подобраны таким образом, чтобы для каждой из 3-х групп условий эксплуатации усредненное значение предельной относительной деформации бетона
, позволяющую учесть класс тяжелого бетона по прочности на сжатие от B10 до B60, а также принадлежность к одной из трех групп по условиям его длительной эксплуатации. Для построения такой зависимости используем алгебраическое выражение, аналогичное (4), в котором числовые коэффициенты подобраны таким образом, чтобы для каждой из 3-х групп условий эксплуатации усредненное значение предельной относительной деформации бетона  соответствовало рекомендациям, приведенным в СП 63.13330:
соответствовало рекомендациям, приведенным в СП 63.13330:
– для благоприятных условий длительной эксплуатации:
 (30)
(30)
– при нормальных условиях эксплуатации:
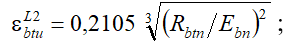 (31)
(31)
– для неблагоприятных условий эксплуатации:
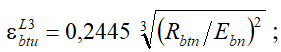 (32)
(32)
Теперь решение системы уравнений (27) - (30) становится возможным. Для их совместного решения используется разработанная программа для ЭВМ. Были рассчитаны искомые величины деформативно-прочностных характеристик тяжелых бетонов различных классов по прочности на сжатие для каждой из 3-х групп условий их эксплуатации (Eb2, 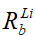 ,
,  ,
,  ,
, ). Некоторые результаты расчетов, выполненных с помощью этой программы, представлены в таблицах 2 и 3.
). Некоторые результаты расчетов, выполненных с помощью этой программы, представлены в таблицах 2 и 3.
Таблица 2
Результаты расчетов деформативно-прочностных характеристик бетонов применительно к неоднородному длительному сжатию с учетом влажностных условий на завершающем этапе эксплуатации зданий непроизводственного назначения
|
Класс бетона |
Rbn, МПа |
Ebn, МПа |
Eb1 Eb2 (МПа) |
|
|
|
|
|
|
|
|
B10 |
7,5 |
19000 |
23650 57120 |
0,00161 0,00301 |
0,00341 |
0,00390 |
0,00455 |
6,4 0,86 |
5,5 0,74 |
4,6 0,62 |
|
B15 |
11,0 |
24000 |
29480 71980 |
0,00170 0,00315 |
0,00358 |
0,00409 |
0,00478 |
9,4 0,85 |
8,0 0,73 |
6,7 0,61 |
|
B20 |
15,0 |
27500 |
33220 82090 |
0,00180 0,00332 |
0,00380 |
0,00434 |
0,00507 |
12,7 0,85 |
10,8 0,72 |
9,0 0,60 |
|
B25 |
18,5 |
30000 |
35780 89120 |
0,00187 0,00345 |
0,00396 |
0,00452 |
0,00528 |
15,6 0,84 |
13,2 0,71 |
11,0 0,59 |
|
B30 |
22,0 |
32500 |
38380 96110 |
0,00193 0,00355 |
0,00408 |
0,00466 |
0,00544 |
18,4 0,84 |
15,6 0,71 |
13,0 0,59 |
|
B35 |
25,5 |
34500 |
40340 101510 |
0,00199 0,00364 |
0,00420 |
0,00480 |
0,00561 |
21,2 0,83 |
18,0 0,70 |
15,0 0,59 |
|
B40 |
29,0 |
36000 |
41670 105310 |
0,00205 0,00374 |
0,00433 |
0,00494 |
0,00577 |
24,0 0,83 |
20,3 0,70 |
16,9 0,58 |
|
B45 |
32,0 |
37000 |
42470 107640 |
0,00210 0,00381 |
0,00443 |
0,00506 |
0,00591 |
26,3 0,82 |
22,3 0,70 |
18,5 0,58 |
|
B50 |
36,0 |
38000 |
43140 109680 |
0,00216 0,00392 |
0,00457 |
0,00522 |
0,00609 |
29,4 0,82 |
24,9 0,69 |
20,6 0,57 |
|
B55 |
39,5 |
39000 |
43900 111820 |
0,00221 0,00399 |
0,00467 |
0,00533 |
0,00623 |
32,1 0,81 |
27,1 0,69 |
22,4 0,57 |
|
B60 |
43,0 |
39500 |
44060 112370 |
0,00226 0,00408 |
0,00478 |
0,00546 |
0,00638 |
34,7 0,81 |
29,3 0,68 |
24,2 0,56 |
Анализ представленных в таблице 2 результатов, показывает, что величины предельных относительных деформаций при центральном (эталонном) сжатии ebR, найденные по предложенной формуле (3), возрастают от 0,00161 для бетона класса B10 до 0,00226 для бетона B60. То есть принятое в СП 63.13330 постоянное значение eb0 = 0,002 примерно соответствует классу бетона В35.
Значения предельных относительных деформаций бетона при неоднородном кратковременном сжатии ebu также возрастают с ростом прочности бетона и укладываются в диапазон от 0,00301 до 0,00408. Таким образом, согласно приведенным в таблице 2 данным, нормируемая величина eb2 = 0,0035 соответствует классу бетона B30.
Соответственно, отношение анализируемых параметров (ebu / ebR) также не является постоянной величиной, которая уменьшается от 1,87 для бетона класса B10 до 1,80 для B60.
Указанные выше тенденции сохраняются и для величин предельных относительных деформаций бетона при неоднородном длительном сжатии  (где i = 1, 2, 3). При этом для благоприятных условий эксплуатации бетона значения параметров
(где i = 1, 2, 3). При этом для благоприятных условий эксплуатации бетона значения параметров  оказались в 1,33 раза меньше по отношению к соответствующим величинам
оказались в 1,33 раза меньше по отношению к соответствующим величинам  , полученным применительно к неблагоприятным условиям эксплуатации. Рекомендованные СП 63.13330 усредненные значения предельной относительной деформации бетона для 3-х групп условий эксплуатации наиболее близко соответствуют классу B35.
, полученным применительно к неблагоприятным условиям эксплуатации. Рекомендованные СП 63.13330 усредненные значения предельной относительной деформации бетона для 3-х групп условий эксплуатации наиболее близко соответствуют классу B35.
Что касается представленных в таблице 2 величин предельных сопротивлений бетонов при длительном неоднородном сжатии  (где i = 1, 2, 3), то можно отметить, что усредненный коэффициент снижения прочности, принятый в СП 63.13330 равным 0,69, можно применять только к бетону, эксплуатация которого осуществлялась в нормальных условиях. При благоприятных условиях эксплуатации указанный коэффициент оказался заметно выше (от 0,81 при классе бетона B60 до 0,86 при B10). А для неблагоприятных условий эксплуатации наблюдается обратная тенденция: все рассчитанные коэффициенты оказались меньше, чем усредненный коэффициент снижения прочности, принятый в СП 63.13330 равным 0,69. В частности, указанный коэффициент изменяется от 0,56 для класса бетона B60 до 0,62 при B10.
(где i = 1, 2, 3), то можно отметить, что усредненный коэффициент снижения прочности, принятый в СП 63.13330 равным 0,69, можно применять только к бетону, эксплуатация которого осуществлялась в нормальных условиях. При благоприятных условиях эксплуатации указанный коэффициент оказался заметно выше (от 0,81 при классе бетона B60 до 0,86 при B10). А для неблагоприятных условий эксплуатации наблюдается обратная тенденция: все рассчитанные коэффициенты оказались меньше, чем усредненный коэффициент снижения прочности, принятый в СП 63.13330 равным 0,69. В частности, указанный коэффициент изменяется от 0,56 для класса бетона B60 до 0,62 при B10.
Таблица 3
Результаты расчетов деформативно-прочностных характеристик бетонов применительно к неоднородному длительному растяжению
|
Класс бетона |
Rbtn, МПа |
|
|
|
|
|
|
|
|
B10 |
0,85 |
0,0000724 0,000131 |
0,000231 |
0,000265 |
0,000308 |
0,406 0,478 |
0,346 0,407 |
0,291 0,342 |
|
B15 |
1,10 |
0,0000736 0,000132 |
0,000235 |
0,000270 |
0,000313 |
0,523 0,475 |
0,445 0,404 |
0,375 0,341 |
|
B20 |
1,35 |
0,0000771 0,000138 |
0,000246 |
0,000282 |
0,000328 |
0,637 0,472 |
0,541 0,401 |
0,456 0,338 |
|
B25 |
1,55 |
0,0000797 0,000142 |
0,000254 |
0,000292 |
0,000339 |
0,726 0,468 |
0,617 0,398 |
0,520 0,336 |
|
B30 |
1,75 |
0,0000820 0,000146 |
0,000262 |
0,000300 |
0,000349 |
0,816 0,466 |
0,693 0,396 |
0,584 0,334 |
|
B35 |
1,95 |
0,0000847 0,000150 |
0,000270 |
0,000310 |
0,000360 |
0,903 0,463 |
0,768 0,394 |
0,646 0,331 |
|
B40 |
2,10 |
0,0000865 0,000153 |
0,000276 |
0,000317 |
0,000368 |
0,968 0,461 |
0,823 0,392 |
0,692 0,330 |
|
B45 |
2,25 |
0,0000889 0,000157 |
0,000284 |
0,000326 |
0,000378 |
1,032 0,459 |
0,877 0,390 |
0,738 0,328 |
|
B50 |
2,45 |
0,0000924 0,000163 |
0,000295 |
0,000338 |
0,000393 |
1,116 0,456 |
0,947 0,386 |
0,797 0,325 |
|
B55 |
2,60 |
0,0000945 0,000166 |
0,000302 |
0,000346 |
0,000402 |
1,178 0,4531 |
1,000 0,385 |
0,841 0,324 |
|
B60 |
2,75 |
0,0000973 0,000170 |
0,000310 |
0,000356 |
0,000414 |
1,239 0,451 |
1,051 0,382 |
0,884 0,322 |
Приведенные в табл. 3 результаты расчетов деформативно-прочностных характеристик бетонов применительно к неоднородному длительному растяжению показывают тенденции, аналогичные тем, что выявлены при неоднородном сжатии (см. табл. 2).
Значения предельных относительных деформаций бетона при неоднородном кратковременном растяжении ebtu также возрастают с ростом прочности бетона и укладываются в диапазон от 0,000131 до 0,000170. Таким образом, согласно представленным в табл. 3 результатам, приведенная в СП 63.13330 усредненная величина ebt2 = 0,00015 соответствует классу бетона B35.
Отношение анализируемых параметров (ebtu / ebtR) не является постоянной величиной, которая изменяется от 1,81 для бетона класса B10 до 1,75 для B60. Аналогичные тенденции сохраняются и для величин предельных относительных деформаций бетона при неоднородном длительном растяжении 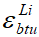 (где i = 1, 2, 3). Рекомендованные СП 63.13330 усредненные значения предельной относительной деформации бетонов для 3-х групп влажностных условий окружающей среды наиболее близко соответствуют классу B35.
(где i = 1, 2, 3). Рекомендованные СП 63.13330 усредненные значения предельной относительной деформации бетонов для 3-х групп влажностных условий окружающей среды наиболее близко соответствуют классу B35.
Анализируя представленные в табл. 3 величины предельных сопротивлений бетонов при длительном растяжении  (где i = 1, 2, 3), можно отметить, что усредненный коэффициент снижения прочности, принятый в СП 63.13330 равным 0,60, существенно завышен даже для бетона, эксплуатация которого осуществлялась в благоприятных условиях, то есть при постоянной относительной влажности воздуха в окружающей среде свыше 75 %. В частности, рассчитанные коэффициенты
(где i = 1, 2, 3), можно отметить, что усредненный коэффициент снижения прочности, принятый в СП 63.13330 равным 0,60, существенно завышен даже для бетона, эксплуатация которого осуществлялась в благоприятных условиях, то есть при постоянной относительной влажности воздуха в окружающей среде свыше 75 %. В частности, рассчитанные коэффициенты  для этих условий эксплуатации оказались заметно ниже 0,60 и находились в диапазоне от 0,451 при классе бетона B60 до 0,478 при B10. А для неблагоприятных условий эксплуатации (относительная влажность воздуха ниже 40%) значения коэффициентов
для этих условий эксплуатации оказались заметно ниже 0,60 и находились в диапазоне от 0,451 при классе бетона B60 до 0,478 при B10. А для неблагоприятных условий эксплуатации (относительная влажность воздуха ниже 40%) значения коэффициентов 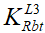 оказались еще ниже и изменялись в интервале от 0,322 для класса бетона B60 до 0,342 при B10.
оказались еще ниже и изменялись в интервале от 0,322 для класса бетона B60 до 0,342 при B10.
Выводы
1. Представлена разработанная авторами методика определения деформативно-прочностных характеристик бетонов как при эталонном кратковременном нагружении, так и при неоднородном деформировании в составе несущих железобетонных конструкций в конце заданного срока их службы в каркасных зданиях непроизводственного назначения с учетом влажностных условий окружающей среды.
2. Выполненные численные исследования показали, что с помощью разработанной методики можно получить основанные на энергетических соотношениях параметры диаграмм длительного неоднородного сжатия и растяжения бетонов, на основании которых будут выполняться уточненные расчеты прочности, трещиностойкости и деформативности (прогибов) несущих конструкций. Это позволит принимать обоснованные решения о целесообразности дальнейшей эксплуатации объекта, его реконструкции или о его сносе (демонтаже), то есть полноценно управлять жизненным циклом рассматриваемого здания с железобетонным каркасом при трех режимах влажностных условий окружающей среды.
1. Almazov V.O. Designing reinforced concrete structures according to European standards [Proektirovanie zhelezobetonnyh konstrukcij po Evronormam]: scientific publication. Moscow: Publishing house of the Association of Construction Universities, 2011. 216 p. (rus)
2. Chirkov V.P. About the determination of the design resistances of concrete for a given service life of the structure [K opredeleniyu raschetnyh soprotivlenij betona pri zadannom sroke sluzhby konstrukcii]. News of higher educational institutions. Construction. 1994. No. 9–10. Pp. 3–7. (rus)
3. Kodysh E.N., Nikitin I.K., Trekin N.N. Calculation of reinforced concrete structures made of heavy concrete in terms of strength, crack resistance and deformation [Raschet zhelezobetonnyh konstrukcij iz tyazhyologo betona po prochnosti, treshchinostojkosti i po deformaciyam]. Moscow: Publishing house of the Association of Construction Universities, 2011. 352 p. (rus)
4. Geniev G.A., Kolchunov V.I., Klyueva N.V., Nikulin A.I., Pyatikrestovskij K.P. Strength and deformability of reinforced concrete structures under beyond design impacts [Prochnost' i deformativnost' zhelezobetonnyh konstrukcij pri zaproektnyh vozdejstviyah]: scientific publication. Moscow: Publishing house of the Association of Construction Universities, 2004. 216 p.
5. Suleymanova L.A. The behavior of concrete under load, the mechanism of its destruction and the assessment of this process [Povedenie betona pod nagruzkoj, mekhanizm ego razrusheniya i ocenka etogo processa]. Bulletin of BSTU named after Shukhov. 2016. No. 1. Pp. 68–75. (rus)
6. Karpenko N.I. General models of reinforced concrete mechanics [Obshchie modeli mekhaniki zhelezobetona]. Moscow: Strojizdat, 1996. 416 p. (rus)
7. Bondarenko V.M. Some issues of the nonlinear theory of reinforced concrete [Nekotorye voprosy nelinejnoj teorii zhelezobetona]. Har'kov: Publishing house of KHSU, 1968. 324 p. (rus)
8. Adishchev V.V., Berezina E.V., Ershova N.V. Determination of transformation coefficients of reference diagrams for bent and non-centrally compressed reinforced concrete elements [Opredelenie koefficientov transformacii etalonnyh diagramm dlya izgibaemyh i vnecentrenno szhatyh zhelezobetonnyh elementov]. News of higher educational institutions. Construction. 2011. No.7. Pp. 73–81. (rus)
9. Merkulov S.I. Fundamentals of the theory of reinforced concrete reconstruction [Osnovy teorii rekonstrukcii zhelezobetona]: monograph. Kursk: Kursk State University, 2009. 248 p. (rus)
10. Mitasov V.M., Adishchev V.V. The main provisions of the energy theory of resistance of reinforced concrete [Osnovnye polozheniya energeticheskoj teorii soprotivleniya zhelezobetona]. News of higher educational institutions. Construction. 2010. no. 6. Pp. 3–7. (rus)
11. Nikulin A.I. An energetic approach to the transformation of reference concrete compression diagrams [Energeticheskij podhod k transformirovaniyu etalonnyh diagramm szhatiya betona]. Concrete and reinforced concrete. 2013. No. 5. Pp. 12–14. (rus)
12. Nikulin A.I., Frolov N.V., Nikulina Yu.A. Crack resistance of bending reinforced concrete elements taking into account the use of various combinations of steel and fiberglass reinforcement in the tension zone [Treshchinostojkost' izgibaemyh zhelezobetonnyh elementov s uchetom ispol'zovaniya v rastyanutoj zone razlichnyh sochetanij stal'noj i stekloplastikovoj armatury]. Concrete and reinforced concrete. 2015. No. 3. Pp. 18–22.
13. Nesvetaev G.V. About the creation of a regulatory framework for concrete deformations under axial loading [K sozdaniyu normativnoj bazy deformacij betona pri osevom nagruzhenii]. News of higher educational institutions. Construction. 1996. No. 8. Pp. 122–124. (rus)
14. Karpenko N.I., Sokolov B.S., Radaykin O.V. Design of concrete, reinforced concrete, stone and reinforced stone elements and structures using diagrammatic calculation methods [Proektirovanie betonnyh, zhelezobetonnyh, kamennyh i armokamennyh elementov i konstrukcij s primeneniem diagrammnyh metodov rascheta]: monograph. Moscow: Publishing house of the Association of Construction Universities, 2019. 194 p. (rus)
15. Zalesov A.S., Muhamediev T.A., Chistyakov E.A. Calculation of crack resistance of reinforced concrete structures according to new regulatory documents [Raschet treshchinostojkosti zhelezobetonnyh konstrukcij po novym normativnym dokumentam]. Concrete and reinforced concrete. 2002. No. 5. Pp. 15–19. (rus)
16. Nikulin A.I. About clarifying the values of the marginal relative deformations of concrete in the compressed zone of bent reinforced concrete elements [K utochneniyu velichin predel'nyh otnositel'nyh deformacij betona v szhatoj zone izgibaemyh zhelezobetonnyh elementov]. Industrial and civil engineering. 2014. No. 8. Pp. 12–15. (rus)
17. Krus' Yu.A. Transformation of concrete deformation diagrams under central compression and tension [Transformirovanie diagramm deformirovaniya betona pri central'nom szhatii i rastyazhenii]. News of higher educational institutions. Construction. 2008. No.7. Pp. 113–122. (rus)
18. Chajka V.P. Characteristics of diagrams of heterogeneous concrete compression [Harakteristika diagramm neodnorodnogo szhatiya betona]. Concrete and reinforced concrete. 1994. No. 1. Pp. 17–19. (rus)
19. Nikulin A.I., Obernikhin D.V., Nikulina Yu.A. Ultimate strength of bent reinforced concrete elements based on the application of the energy criterion of concrete destruction [Predelynaya prochnost izgibaemyh zhelezobetonnyh elementov na osnove primeneniya energeticheskogo kriteriya razrusheniya betona]. Security of the construction fund in Russia. Problems and Solutions: Materials of International Academic Readings. Kursk: Kursk State University, 2014. Pp. 98–107. (rus)
20. Berg O.Ya. Physical fundamentals of the theory of strength of concrete and reinforced concrete [Fizicheskie osnovy teorii prochnosti betona i zhelezobetona]. Moscow: Gosstrojizdat, 1962. 96 p.