Ufa, Russian Federation
UDC 004.9
UDC 378.1
This article discusses the application of neural networks in managing the educational trajectory in electronic educational systems. A model of learning management in an electronic information and educational environment is built, and an algorithm for managing adaptive learning is described. A test example of a neural network is constructed, showing the capabilities and problems of applying neural networks to the tasks of constructing trajectories of students’ adaptive personalized training. The following stages of constructing a neural network model are implemented: determining the structure of a neural network and its software implementation using the PyTorch deep machine learning library; preparing a test training sample for training the neural network; importing the initial data for training the model using the modules of the Pandas library; training the model using torch.optim Adam, Adamax, and Rprop optimizers; visualizing the obtained data in the form of graphs based on the matplotlib library; exporting the obtained numerical results and analysing the data. The paper also states the problems of preparing a training data set for teaching a neural network. The paper concludes that using neural networks in the field of building personalized adaptive educational trajectories has great prospects and will be one of the urgent tasks in the coming years.
learning trajectory, e-learning, neural network, modeling, PyTorch
Введение
Построение адаптивных образовательных траекторий с учетом личности обучаемых – одно из современных требований принципа гуманизации образования, предусматривающего создание максимально возможных условий для развития личности. Этот принцип должен лежать и в основе педагогического дизайна, ориентированного на создание современных электронных образовательных систем с использованием новейших информационных технологий, в том числе, и с применением нейронных сетей.
Вопросы применения нейронных сетей для реализации персонализированного адаптивного обучения студентов рассматривают многие современные авторы, например, Босов А.В., 2022 [1], Чумакова Е.В., Корнеев Д.Г., Гаспариан М.С., 2022 [2], Luo Q., Yang J., 2022 [3], Okewu E., Adewole P., Misra S., Maskeliunas R., Damasevicius R., 2021 [4], Fiore U., 2019 [5], Lee Y., 2019 [6], Бакунова О.М., Калитеня И.Л., Бакунов А.М., Палуйко А.Ф., Антонов Е.Д., Гречко И.С., 2018 [7], Мицель А.А., Погуда А.А., Семенов К.А., Утешева А.Е., 2013 [8] и др.
Но, тем не менее, на основании анализа литературы можно сделать вывод, что в настоящее время методология нейросетевого моделирования носит в основном исследовательский характер. Нет единой концепции выбора структуры и параметров нейросетевых моделей, отсутствует научное обоснование критериев оптимальности в построении узлов адаптивной образовательной траектории.
Цель данного исследования – изучить вопросы управления траекторией электронного обучения с применением нейросетевых технологий, а также реализовать тестовую нейросетевую модель построения адаптивной образовательной траектории в электронном курсе.
1. Материалы и методы
Рассмотрим задачу построения образовательной траектории в Электронной информационно-образовательной среде (ЭИОС) с точки зрения автоматизированной системы управления.
Будем считать, что ЭИОС выступает как устройство управления и при этом получает разнообразную информацию о текущем состоянии процесса обучения (рис. 1).
Обозначим:
X=(x1, x2, … xn) – множество параметров обучающих воздействий внешней среды;
Y=(y1, y2, … ym) – множество параметров состояния обучающегося;
R=(r1, r2, … rt) – параметры ресурсов управляющей системы в виде ресурсов ее базы знаний;
P=(p1,p2, … ps) – параметры профессиональной компетентности обучающегося как множество новых знаний и умений, полученных при обучающем воздействии U внешней среды;
DX и DY – индикаторы текущего состояния электронной информационно-образовательной среды.
Управляющее воздействие U видоизменяет текущие параметры обучаемого согласно заданного критерия оптимизации. Взаимодействие с компетентностной моделью обучаемого позволяет при этом реализовывать выбор оптимальной образовательной траектории, обеспечивающей цели управления [9].
Далее обозначим: Р* – цель обучения в виде максимального достижения уровня профессиональной компетентности обучаемого; Y* – наилучшее (максимальное) значение обучения.
Задача управляющей системы – используя оперативный анализ параметров управления достичь наилучшего значения обучения Y*, т. е. <X, Y, R, Р*> ® U ® Y*.
Алгоритм управления адаптивным обучением при этом может представлять собой следующую последовательность шагов:
- начало обучения – идентификация обучаемого в системе;
- проверка начального уровня обученности;
- построение стартовой компетентностной модели обучаемого;
- подбор модуля для последующего обучения с учетом компетентностной модели обучаемого;
- адаптивный подбор задания для выполнения;
- анализ результатов выполнения задания;
- сопоставление цифрового следа обучения с индикаторами усвоения компетенций;
- оценка текущего уровня сформированности компетенции с точки зрения знаний, умений, навыков и соответствующих личностных профессиональных качеств (в том числе, выполнение задания в установленный заданный срок, ритмичность самостоятельной работы и т.д.);
- при прохождении обучающимся порогового уровня сформированности компетенций – переход к подбору следующего задания для выполнения, иначе – возврат к дополнительному повторному изучению материала и повторное прохождение задания;
- при успешном выполнении всех требуемых заданий модуля – переход к подбору следующего модуля обучения;
- при завершении всех модулей обучения – построение итоговой компетентностной модели обучаемого.
В качества входных данных подсистемы подбора заданий в модели адаптивного обучения при этом могут использоваться сведения о предыдущих достижениях обучающегося, например:
- тематика ранее пройденных вопросов, заданий и их количество по каждой из тем, с учетом наличия связи между темами;
- данные о результатах оценки за выполненные тесты и задания с учетом их уровня сложности;
- данные о времени, потраченном на ответы и пр.
Очевидно, что практическая реализация нейросетевых систем данного класса является очень сложной задачей и может быть решена в настоящее время пока только на уровне тестовых моделей.
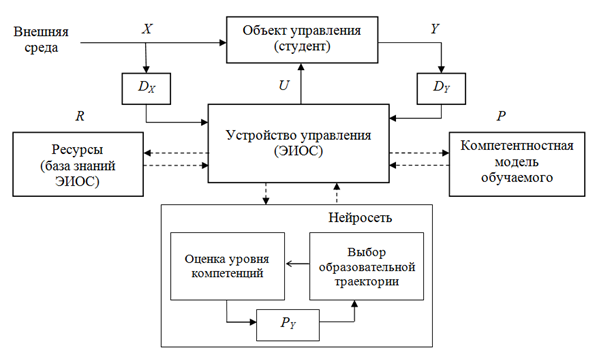
Рис.1. Управление обучением в электронной информационно-образовательной среде (ЭИОС)
Fig.1. Training management in the electronic information and educational environment
2. Результаты
Был построен тестовый пример нейронной сети, показывающий возможности и проблемы применения нейронных сетей к задачам построения траекторий адаптивного персонализированного обучения студентов.
При этом были реализованы следующие этапы построения нейросетевой модели:
- определение структуры нейронной сети и ее программная реализация с применением библиотеки глубокого обучения PyTorch;
- подготовка тестовой обучающей выборки для обучения нейронной сети;
- импорт исходных данных для обучения модели с использованием модулей библиотеки Pandas;
- обучение модели с применением оптимизаторов torch.optim Adam, Adamax и Rprop;
- визуализация полученных данных в виде графиков на основе библиотеки matplotlib;
- экспорт полученных численных результатов и анализ данных.
Топология нейронной сети имеет три слоя, в качестве функции активации использовалась Sigmoid, число нейронов в скрытом слое изменялось в ходе экспериментов от 30 до 50.
Были использованы три разных варианта оптимизаторов, позволяющих реализовывать шаги градиентного спуска:
- torch.optim.Adam, основанный на алгоритме Адама (характеризуется Kingma D.P., Ba J. в [10] как высоко эффективный метод стохастической оптимизации, который является не требовательным к памяти и хорошо устойчивым к изменению масштаба градиентов);
- torch.optim.Adamax, основанный на алгоритме Адамакс (представляет собой один из вариантов Адама, основанного на норме бесконечности);
- torch.optim.Rprop, широко описанный в литературе устойчивый алгоритм обратного распространения (например, описывается Igel C., Hüsken M. в [11] как один из эффективных алгоритмов обучения первого порядка для нейросетевых моделей с произвольной топологией).
Для дальнейшего обучения нейросетевой модели был подготовлен массив данных размерностью 1000 строк и 10 столбцов.
Данные были сгенерированы по рандомно зашумленному закону в виде полиномиальной функции в диапазоне от 0 до 100. Данный массив тем самым воспроизводит идею числовой балльной оценки выполненных заданий (либо некую возможную числовую характеристику параметров модели личности обучаемого).
Надо заметить, что построение настоящего обучающего множества представляет собой крайне сложную задачу ввиду необходимости научного обоснования оптимальности предлагаемой адаптивной образовательной траектории. В настоящее время это является одним из наиболее слабых мест в применении нейронных сетей при проектировании адаптивных обучающих ресурсов [12].
На рис. 2-4 приводятся полученные экспериментальные результаты исследования качества обучения сети с помощью анализа динамики функции потерь (loss) для метода градиентного спуска.
Было получено, что при параметре скорости обучения lr=0.01 оптимально-достаточным количеством эпох обучения является 2000 эпох. При этом была достигнута сходимость метода градиентного спуска всеми оптимизаторами (Adam, Adamax и Rprop).
Как видим из рис. 2, метод Rprop обеспечил самую быструю сходимость градиентного спуска. Таким оптимизаторам как Adam и Adamax понадобилось значительно большее, но сопоставимое число эпох.
Далее было проведен компьютерный эксперимент по исследованию устойчивости работы нейросети при изменении следующих параметров оптимизатора Adam:
- изменение коэффициента скорости обучения lr от 0.01 до 0.1;
- увеличение количества нейронов в скрытом слое от 30 до 50.
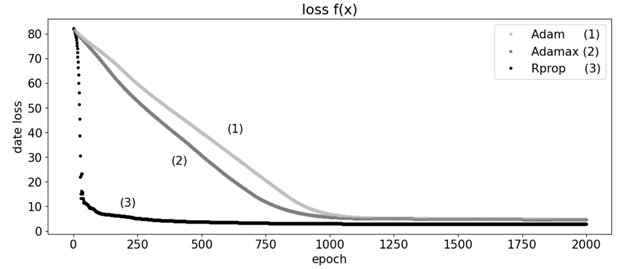
Рис. 2. График исследования сходимости модели при скорости обучения lr=0.01 (количество нейронов скрытого слоя 30)
Fig. 2. Graph for studying the convergence of the model at a learning rate of lr=0.01 (the number of neurons in the hidden layer is 30)
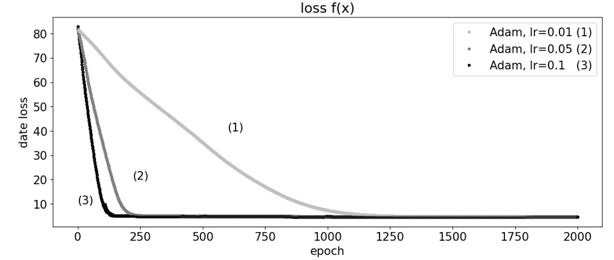
Рис. 3. График исследования сходимости модели при изменении скорости обучения от lr=0.01 до lr=0.1 (количество нейронов скрытого слоя 30)
Fig. 3. Graph for studying the convergence of the model when the learning rate changes from lr=0.01 to lr=0.1 (the number of hidden layer neurons is 30)
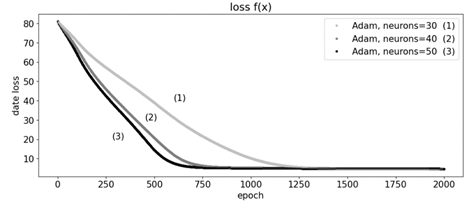
Рис. 4. График сходимости модели при изменении количества нейронов скрытого слоя от 30 до 50 (скорость обучения lr=0.01)
Fig. 4. Graph of model convergence when changing the number of hidden layer neurons from 30 to 50 (learning rate lr=0.01)
Из рис. 3 видим, что увеличение параметра скорости обуения lr от 0.01 до 0.1 значительно улучшает качество работы оптимизаторов Adam.
Как видим из рис. 4, при параметре скорости обучения lr=0.01 изменение числа нейронов скрытого слоя с 30 до 50 приводит к увеличению скорости метода градиентного спуска. Но при этом надо понимать, что увеличение числа нейронов приводит к усложнению топологии сети, что может привести к ухудшению ее обучения в случае большого количества слоев.
Данный пример показывает возможность применения нейросетевых моделей в задачах выбора дальнейших узлов индивидуальной траектории обучения с использованием информации о пройденных узлах электронного курса.
Заключение
Педагогический дизайн – это сравнительно новое направление в проектировании обучающих электронных ресурсов, ориентированное на учет всех требований концепции обеспечения наилучших условий для развития личности обучаемого. При этом очевидно, что разработка современных обучающих ресурсов требует использования разнообразных интеллектуальных информационных технологий. Одним из примеров таких технологий может стать нейросетевое моделирование, предполагающее использование методов глубокого машинного обучения при разработке образовательных систем.
В ходе данной работы была разработана модель управления обучением в электронной информационно-образовательной среде с применение нейросетевых технологий, были рассмотрены особенности управления адаптивным обучением, а также описаны этапы проектирования и обучения модельного примера нейронной сети, позволяющей строить образовательную траекторию с учетом предыдущих достижений обучающегося. При построение данного примера использовалась библиотека глубокого машинного обучения PyTorch и модули библиотек Pandas и matplotlib.
Были проведены исследования данной построенной нейронной сети с точки зрения подбора оптимальных параметров ее обучения. Было установлено, что для обучения данной сети достаточно использовать около 2000 эпох. При этом также были изучены такие параметры как скорость обучения и число нейронов в скрытом слое. Экспериментально было получено, что увеличение параметра скорости обучения lr от 0.01 до 0.1 значительно улучшает качество работы оптимизаторов Adam. Так же было получено, что увеличение числа нейронов скрытого слоя с 30 до 50 увеличивает скорость обучения сети. Отмечается, что дальнейшее значительное увеличение числа нейронов может привести к усложнению топологии сети, что приведет к ухудшению ее обучения в случае большого количества слоев.
Самой большой проблемой, связанной с обучение нейронных сетей задачам построения адаптивных образовательных траекторий, является проблема построения обучающего набора данных с точки зрения критериев оптимальности обучения. На данный момент отсутствуют общие научно обоснованные критерии оптимальности выбора следующего узла адаптивной траектории, что делает задачу построения обучающей выборки крайне сложной и многозначной. Но, тем не менее, очевидно, что применение нейронных сетей в области построения персонализированных адаптивных образовательных траекторий имеет большие перспективы и будет являться одной из актуальных задач ближайших лет.
1. Bosov A.V. Application of Self-Organizing Neural Networks to the Process of Forming an Individual Learning Path. Informatics and Applications. 2022;16(3):7-15. DOIhttps://doi.org/10.14357/19922264220302.
2. Chumakova E.V., Korneev G.A., Gasparian M.S. Development of Adaptive Testing Method Based on Neurotechnologies. Open Education. 2022;26(2):4-13. DOIhttps://doi.org/10.21686/1818-4243-2022-2-4-13.
3. Luo Q., Yang J. The Artificial Intelligence and Neural Network in Teaching. Computational Intelligence and Neuroscience. 2022;2022(1):1-11. DOIhttps://doi.org/10.1155/2022/1778562.
4. Okewu E, Adewole P, Misra S, et al. Artificial Neural Networks for Educational Data Mining in Higher Education: A Systematic Literature Review. Applied Artificial Intelligence. 2021;35(13):983-1021. DOIhttps://doi.org/10.1080/08839514.2021.1922847.
5. Fiore U. Neural Networks in the Educational Sector: Challenges and Opportunities. Balkan Region Conference on Engineering and Business Education. 2019;1:332-337. DOIhttps://doi.org/10.2478/cplbu-2020-0039.
6. Lee Y. Using Self-Organizing Map and Clustering to Investigate Problem-Solving Patterns in the Massive Open Online Course: An Exploratory Study. Journal of Educational Computing Research. 2019;57(2):471-490. DOIhttps://doi.org/10.1177/0735633117753364.
7. Bakunova O.M., Kalitenya I.L, Bakunov A.M., et al. The Use of Neural Networks in Education. Web of Scholar. 2018;1-1(19):8-10.
8. Mitsel A.A., Poguda A.A., Seienov K.A., et al. Testing Methods of Knowledge on the Basis of Neural Network. Open Education. 2013;2(97):34-41. DOIhttps://doi.org/10.21686/1818-4243-2013-2(97)-34-41.
9. Minasova N.S., Tarkhov S.V., Tarkhova L.M. Content Management of Aggregated Training Modules in E-Learning Systems Based on the Image Structuring Method. System Engineering and Information Technologies. 2019;1-1(1):54-62.
10. Kingma D.P., Ba J. Adam: A Method for Stochastic Optimization. In: Proceedings of the 3rd International Conference on Learning Representations (ICLR); San Diego: 2015. DOIhttps://doi.org/10.48550/arXiv.1412.6980.
11. Igel C., Hüsken M. Empirical Evaluation of the Improved Rprop Learning Algorithms. Neurocomputing. 2003;50:105-123. DOIhttps://doi.org/10.1016/S0925-2312(01)00700-7.
12. Shamsutdinova T.M. Problems and Prospects for the Application of Neural Networks for the Sphere of Education. Open Education. 2022;26(6):4-10. DOIhttps://doi.org/10.21686/1818-4243-2022-6-4-10.














