Rostov-na-Donu, Rostov-on-Don, Russian Federation
Rostov-na-Donu, Rostov-on-Don, Russian Federation
Russian Federation
Don State Technical University (Undergraduate)
Donskoy gosudarstvennyy tenicheskiy universitet
Russian Federation
VAC 05.23.01 Строительные конструкции, здания и сооружения
VAC 05.23.17 Строительная механика
UDK 69 Строительство. Строительные материалы. Строительно-монтажные работы
GRNTI 67.11 Строительные конструкции
GRNTI 67.01 Общие вопросы строительства
OKSO 270000 АРХИТЕКТУРА И СТРОИТЕЛЬСТВО
BBK 385 Строительные конструкции
BBK 308 Монтаж, эксплуатация, ремонт машин и промышленного оборудования
BISAC TEC009020 Civil / General
The article discusses the modeling of the nonlinear work of the material of the floor slab of a monolithic frame building. Two laws of the deformation of materials in the calculation by the finite element method are investigated. An analysis of the influence of the laws of deformation on the deflections of the floor slab, the main stresses and the destruction schemes of the floor slab by layers allowed us to give recommendations on the consideration of the nonlinear properties of materials when performing strength calculations.
finite element method, physical nonlinearity, material deformation law, exponential dependence, stress-strain state
При проектировании современных зданий и сооружений необходимо учитывать не только требования безопасности, но и экономичности. Один из вариантов снижения расхода материалов и повышения надежности конструктивных решений проектируемого объекта соответствует использованию точных методов оценки напряженно-деформированного состояния, учитывая специфические свойства железобетона, таких как трещинообразование, , пластические деформации бетона и арматуры.
Развитию методов нелинейных расчета конструкций посвящено достаточное количество теоретических и экспериментальных работ. Но при этом нет единой методики расчета конструкций, с помощью которой можно оценить их напряженно-деформированное состояние на всех этапах нагружения вплоть до стадии разрушения.
Конечные элементы тонких пластин используют для прочностного расчета с учетом физической нелинейности материала. Элементы матрицы жесткости конечного элемента определяют по форме:
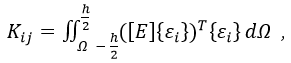
где: Ω - область конечного элемента;
[Е] - матрица интегральных жесткостей k-го шага;
{ε} - вектор деформаций.
В нелинейных расчетах применяется шагово-итерационный метод с расчетом новых значений модуля Юнга и приведенного коэффициента Пуассона по выбранному пользователем закону деформирования материала на основании определенной в данной точке обобщенной деформации.
Для зависимости, показанной на Рис.1а, задается предельное значение деформации и коэффициента запаса по обобщенному напряжению вручную. Экспоненциальная зависимость может применяться для основного и армирующего материала конструкции и формируется автоматически в программном комплексе (рис. 1б).
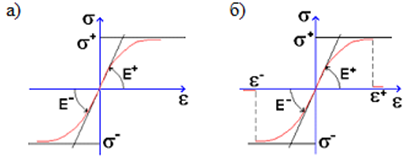
Рис. 1. Законы деформации материалов: а) значения характеристик задаются вручную; б) автоматически в программном комплексе
Выполнено исследование влияния законов деформации на прогибы монолитных плит перекрытия. Объект исследования является двухэтажный монолитный железобетонный каркас здания начальной школы в г. Новочеркасск Ростовской области. Для анализа модели с учетом нелинейной работы материала рассмотрена плита перекрытия подвала. В соответствии с архитектурными решениями исследуемая плита нагружена массивными перегородками высотой 8,5 м. На площади исследуемой плиты расположены душевые комнаты, кабинеты, технические помещения с ограждением кирпичными перегородками.
Расчетная модель разработана по плитно-стрежневой схеме в программном комплексе Лира-САПР. Граничные условия соответствуют закреплению стен и колонн по направлениям степеней свободы (рис. 2).
Рис. 2. Конечно- элементная модель плиты перекрытия подвала
Плита перекрытия моделируется конечными элементами с шестью степенями свободы в узле. При определении напряженно-деформированного состояния конструкций железобетонная оболочка рассматривается как система с изотропным физически нелинейным материалом бетона.
Рассмотрены два варианта экспоненциальных законов нелинейного деформирования материала плиты перекрытия (рис. 3).
Рис. 3. Законы нелинейного деформирования бетона В25:
а) модель 1; б) модель 2
В расчетной модели учтены нагрузки от собственного веса плиты перекрытия, полов, перегородок, ограждающих стен, а также нагрузки, возникающие в процессе эксплуатации здания. Для моделирования нелинейного загружения использован шаговый метод.
В результате расчета получено напряженно-деформированное состояние плиты перекрытия. Максимальный прогиб в зоне концентрации напряжений кирпичных перегородок по первой расчетной модели составляет 8 мм, по второй – 12 мм (рис. 4).
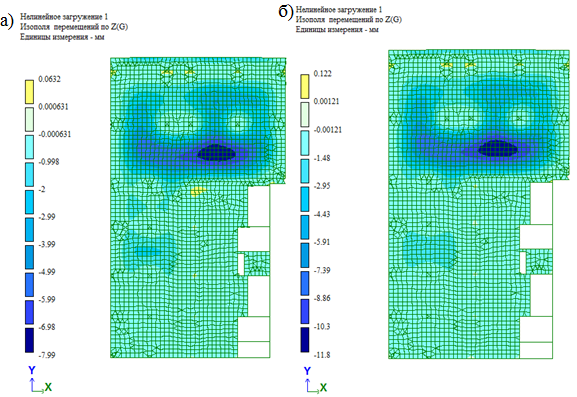
Рис. 4. Прогибы плиты перекрытия: а) модель 1; б) модель 2
Анализ результатов показал, что при использовании закона экспоненциальной зависимости для железобетона (модель 2) прогибы плиты перекрытия увеличились на 48% по сравнению с прогибами, полученными по первой расчетной модели.
Выполнено исследование картины разрушений по верхнему и нижнему слою плиты перекрытия. На рис. 5 и 6 показаны направления развития трещин на фоне изополей главных напряжений.
Рис. 5. Разрушений бетона по верхнему слою: а) модель 1; б) модель 2
Концентрация напряжений соответствует расположению массивных кирпичных перегородок, усиленных армирующей сеткой и металлическими стойками.
Рис. 6. Разрушений бетона по нижнему слою: а) модель 1; б) модель 2
Картина разрушения бетона по верхнему слою соответствует расположению несущих конструкций каркаса здания. Предельное состояние наступает в нижних слоях бетона, не доводя конструкцию до разрушения. Ширина раскрытия трещин соответствует нормативным значениям.
Анализ изолиний главных напряжений позволяет сделать вывод, что напряжения в верхнем слое одинаковы для первого и второго варианта расчетных моделей. Напряжения в нижнем слое плиты перекрытия по второй схеме увеличились на 31 % при автоматическом учете нелинейных свойств бетона.
Площадь развития трещин в зоне расположения массивных перегородок по верхнему слою больше при расчете по второй модели. Раскрытие трещин нижнего слой бетона плиты перекрытия больше по первой модели и не превышает предельных значений.
По результатам исследования можно сделать вывод, что при расчете прогибов и напряжений монолитных железобетонных плит перекрытий достаточно использовать экспоненциальную зависимость, задаваемую программой автоматически. При определении картины разрушений по слоям рекомендуется выполнять расчет с использованием нескольких законов деформирования материалов.
1. Geniev G.A., Kissyuk V.N., Tyupin G.A. Teoriya plastichnosti betona i zhelezobetona - M.:Strojizdat, 1974 - p. 316.
2. Lejtes E.S. K utochneniyu odnogo iz uslovij prochnosti betona. Povedenie betonov i elementov zhelezobetonnyh konstrukcij pri vozdejstvii razlichnoj dlitel'nosti. - M. : NIIZHB, 1980 - p. 37 - 40
3. Yashin A.V. Kriterij prochnosti i deformirovaniya betona pri prostom nagruzhenii dlya razlichnyh vidov napryazhennyh sostoyanij/ Raschet i konstruirovanie zhelezobetonnyh konstrukcij. - M. : Strojizdat, 1977.- p.48-57.
4. Murtazaliev G.M., Pajzulaev M.M. Algoritm rascheta nelinejnogo povedeniya tonkostennyh sistem. Vestnik Dagestanskogo gosudarstvennogo tekhnicheskogo universiteta. Tekhnicheskie nauki. 2019;46(2).- p. 176-184.
5. Agahanov E.K., Kravchenko G.M., Panasyuk L.N., Trufanova E.V. Realizaciya metoda kinematicheskoj dekompozicii dlya raschetov v nelinejnoj postanovke. Vestnik Dagestanskogo gosudarstvennogo tekhnicheskogo universiteta. Tekhnicheskie nauki. 2014;35(4).- p. 14-19.
6. Savost'yanov V.N., Agahanov E.K. Ob ekvivalentnosti vozdejstvij v staticheskoj zadache mekhaniki deformiruemogo tverdogo tela. Izv. Vuzov. Stroitel'stvo. - 1995. - № 10. - p. 26-30.
7. Agahanov E.K., Agahanov M.K., Sultanova L.M., Hizrieva Z.A. Conditions of equivalence of effects for the solid body from incompressible material. MATEC Web of Conferences. 196, 01031 (2018) https://doi.org/10.1051/matecconf/201819601031 XXVII R-S-P Seminar 2018, Theoretical Foundation of Civil Engineering.
8. Kravchenko G.M., Trufanova E.V., Nazarenko D.I., SHaripov E.R. Raschet zdaniya obshchezhitiya tekhnoparka Rostovskogo gosudarstvennogo stroitel'nogo universiteta (RGSU) s primeneniem razlichnyh modelej osnovaniya.- Inzhenernyj vestnik Dona. 2015. № 3 (37). -p. 112.
9. Kravchenko G.M., Trufanova E.V., Dumbaj V.A., Kamesh Yu.A. Issledovanie neravnomernoj osadki osnovaniya sportivno-ozdorovitel'nogo kompleksa tekhnoparka RGSU metodom konechnyh elementov. Inzhenernyj vestnik Dona. 2016. № 1 (40). - p. 42.
10. Panasyuk L.N., Kravchenko G.M., Trufanova E.V. O tochnosti opredeleniya napryazhenno-deformirovannogo sostoyaniya i konstruktivnyh parametrov v oblastyah s osobennostyami.Internet-zhurnal Naukovedenie. 2013. № 3 (16). - p. 101.
