Дедуктивно-аксиоматический метод был и остается основным при построении различных теорий классической математики (эвклидова и неевклидовы геометрии, арифметика натуральных чисел, математический анализ, теория множеств, теория вероятностей, теория структур и др.), а также классической логики (исчисление высказываний, исчисление предикатов, вероятностная логика, модальная логика, деонтическая логика и др.). При построении теорий  конструктивной математики и логики на смену ему пришли такие методы, как конструктивное доказательство, математическая индукция и итерация. Первой научной теорией, построенной дедуктивно-аксиоматическим методом, была геометрия Эвклида, которая долгое время, вплоть до начала XX в., считалась непререкаемым эталоном научности не только в математике, но и в науке в целом [3; 8]. В чём главный смысл и технология дедуктивно-аксиоматического метода? В том, что между некоторыми высказываниями теории, принятыми за исходные (аксиомы теории), и всеми остальными ее высказываниями устанавливается отношение логической выводимости этих высказываний только из аксиом. Формально-логическая выводимость одних высказываний из других в современной логике называется дедукцией. Высказывания, логически не выводимые из аксиом теории, построенной дедуктивно-аксиоматическим методом, не могут считаться принадлежащими данной теории, даже если они являются эмпирически истинными.

Построить теорию дедуктивно-аксиоматическим методом означает установить между всеми ее истинными высказываниями отношение логического замыкания друг на друга. Это – очень сложная задача.  Так на ее  положительное решение для геометрического знания у древнегреческих математиков ушло около трехсот лет (с 7 в. до н.э. до 4 в. до н.э.). Начало этой теоретической работе положил Фалес, а завершил ее Эвклид, имя которого и стала носить первая система теоретической геометрии. В чем научное и эпистемологическое значение применения дедуктивно-аксиоматического построения научной теории. В том, что успешная реализация этого метода делает научную теорию: а) логически доказательной системой знания; б) относительно замкнутой и самодостаточной по отношению к эмпирическому знанию; в) способной развиваться на своей собственной основе. Построение теории дедуктивно-аксиоматическим методом означает также возможность логической редукции всего истинного содержания теории только к содержанию её аксиом и тем самым максимально минимизировать решение проблемы истинности теории, сосредоточив все внимание только на доказательстве истинности только очень небольшого количества утверждений теории – ее аксиом [7; 15].

Необходимо при этом подчеркнуть, что понятия дедуктивный метод и дедуктивно-аксиоматический метод  не являются тождественными. Каково же отношение между ними? Оно таково: всякий дедуктивно-аксиоматический метод является дедуктивным, но не всякий дедуктивный метод является аксиоматическим, поскольку отнюдь не обязательно, чтобы посылки любого дедуктивного вывода были аксиомами, или исходными положениями теории. Очевидно также (и это является одним из главных достоинств использования  дедуктивно-аксиоматического метода при построении научной теории), что подавляющее большинство высказываний научной теории, построенной дедуктивно-аксиоматическим  способом, является аналитическими истинами, не требующих эмпирического обоснования, поскольку их истинность гарантирована их логической выводимостью из аксиом теории. Но как может быть доказана истинность аксиом теории: ведь от положительного решения этого вопроса  зависит вся ценность дедуктивно-аксиоматического метода построения научных теорий. История научного познания говорит о том, что решение этой проблемы могло быть осуществлено и реально осуществлялось четырьмя основными способами:

1) выведением аксиом теории в качестве следствий из другой более общей теории, принятой за истинную;

2) принятие решения об истинности аксиом, благодаря их интуитивной очевидности для мышления в силу простоты их содержания;

3) экспериментальное (опытное) подтверждение истинности аксиом при определенной их эмпирической интерпретации;

4) принятие аксиом в качестве истинных утверждений условно (на основе конвенции или научного консенсуса).

Все эти способы обоснования истинности аксиом реально использовались и используются в науке. Однако, у каждого из них, имеются как свои плюсы, так и свои недостатки.

 Так, при первом способе обоснования истинности аксиом их истинность оказывается только относительной, поскольку напрямую зависит от истинности другой теории, из которой эти аксиомы могут быть выведены в качестве ее следствий. И здесь нас поджидает опасная ловушка логической регрессии в бесконечность. Так, в начале XX в. Б. Рассел, А. Уайтхед попытались вывести аксиомы самой простой и фундаментальной математической теории –  арифметики натуральных чисел – в качестве теорем математической логики. Но тогда очевидно, что доказательство истинности аксиом арифметики стало полностью зависеть от возможности доказательства истинности логических теорий [1; 13]. Другой пример такого же рода. Когда-то, в 70-х годах XIX в., Б. Риман доказал, что аксиомы эвклидовой и неэвклидовых геометрий могут быть получены в качестве следствий  из общей римановой геометрии, в которой кривизна пространства является величиной не постоянной, а переменной. Но тогда истинность аксиом эвклидовой и неэвклидовых геометрий становилась условной, относительной и зависящей от истинности или неистинности общей римановой геометрии [2]. Но самая главная опасность данной ситуации связана с тем, что более общая теория, из которой могут быть выведены аксиомы другой теории, может оказаться логически противоречивой. Именно это и случилось в конце XIX в., когда аксиомы арифметики натуральных чисел вывели в качестве следствий теории множеств Г. Кантора с помощью теоретико-множественного определения натурального числа. Однако впоследствии в теории множеств Кантора были обнаружены логические противоречия (парадоксы множества всех множеств, наибольшего кардинального числа, множества всех нормальных подмножеств и др.), а потому от идеи сведения арифметики к теории множеств отказались [4; 13].

При обосновании же истинности аксиом теории вторым способом – путём апелляции к интуитивной очевидности аксиом, также возникают серьёзные проблемы. Хотя именно таким образом в течение длительного времени, начиная собственно с античности, и обосновывалась истинность аксиом эвклидовой геометрии (Эвклид, Аристотель, Декарт, Кант и др.). Зачастую подобное обоснование истинности аксиом эвклидовой геометрии встречается и в современных монографиях и учебниках по эвклидовой геометрии. Как известно, сам Эвклид положил в основу построенной им геометрии пять следующих аксиом:

1. Отрезок прямой может быть продолжен в обе стороны сколь угодно далеко.

2. Все прямые углы равны.

3. Из точки, как из центра, может быть проведена окружность любого радиуса.

4. Две точки всегда могут быть соединены между собой прямой линией.

5. Если две прямые на плоскости пересечены третьей прямой, то они пересекутся с той стороны третьей прямой, где сумма внутренних односторонних углов, образуемых ею с этими прямыми, меньше 180°[2; 8].

Из этих пяти аксиом Эвклид вывел в качестве следствий, и тем самым доказал, более трехсот других геометрических утверждений (планиметрии и стереометрии). Среди них он логически доказал такие утверждения, как: сумма углов любого треугольника равна 180°; площадь равнобедренного треугольника равна половине произведения основания на высоту; диагонали в прямоугольнике равны; два перпендикуляра к одной прямой при их продолжении никогда не пересекаются; длина любой окружности равна 2πR; площадь любого круга равна πR² и  т.д. При этом  сам Эвклид полагал, что истинность аксиом его геометрии является интуитивно очевидной для разума, хотя истинность большинства из ее теорем вовсе не является таковой. Например, истинность теоремы Пифагора о соотношении гипотенузы и катетов прямоугольного треугольника отнюдь непосредственно не очевидна для разума, а потому требует доказательства путём ее логического выведения в качестве следствия из очевидно истинных и содержательно более простых утверждений  геометрии – ее аксиом.

Отметим также то обстоятельство, что исходные утверждения теории – ее аксиомы, вовсе не обязательно должны состоять только из исходных понятий теории. Как правило, в аксиомы теории входят понятия, обозначающие как  исходные объекты теории, так и ее производные объекты. Например, в аксиомах Эвклида встречаются такие понятия и объекты, как прямой угол, окружность, внутренние односторонние углы. Это – не исходные, а производные понятия и объекты эвклидовой геометрии. Таким образом, редукция (сведение) всех понятий теории к ее исходным понятиям и редукция  всех ее высказываний только к исходным (аксиомам) – это  относительно самостоятельные и относительно независимые познавательные стратегии при дедуктивно-аксиоматическом методе построения научной теории. Но насколько интуитивно очевидными для разума являются аксиомы эвклидовой геометрии? В отношении первых четырех аксиом у математиков действительно никогда не возникало сомнения в их очевидной истинности для разума, благодаря исключительной простоте и ясности содержания этих аксиом. При этом их истинность очевидна именно для мышления, а вовсе не для чувств, поскольку для чувств как раз далеко не очевидно, что отрезок прямой линии всегда может быть продолжен сколь угодно далеко, или то, что из некоторой точки всегда  можно провести окружность любого радиуса. Однако в отличие от первых четырех аксиом геометрии Эвклида ее пятый постулат всегда вызывал у математиков сомнение в его истинности для разума. И поэтому вполне закономерно, что уже начиная с самого Эвклида и вплоть до открытия и принятия неевклидовых геометрий в середине XIX в., в геометрии постоянно предпринимались попытки доказать аксиому о параллельных как теорему и таким образом перевести ее в ранг производных истинных высказываний эвклидовой геометрии. Более того, само возникновение неэвклидовой геометрии имело своим первоначальным толчком именно доказательство необходимости пятого постулата среди других аксиом эвклидовой геометрии. Путь к этому видели один – доказательство логической противоречивости системы геометрических аксиом, в которых пятый постулат Эвклида был бы заменен его отрицанием. Для этого были предприняты шаги по замене пятого постулата Эвклида на тождественное по содержанию, но при этом более простое для мысленного восприятия высказывание. Таких эквивалентных и наиболее простых замен постулата о параллельных было предложено две: 1.Через точку на плоскости нельзя провести более одной прямой, параллельной данной прямой. 2. Через точку на плоскости можно провести только одну прямую, параллельную данной прямой. Именно в последней версии постулат о параллельных линиях позже, начиная с 18 в., войдет во все учебники по геометрии [3]. При этом под параллельными линиями понимались прямые линии, которые при их бесконечном продолжении никогда не пересекутся. При этом второй вариант аксиомы о параллельных Декарт и Кант считали, например, столь же очевидным для разума, как и истинность четырех остальных постулатов. Но для ряда философов и математиков, таких как Лейбниц, Саккери, Ламберт, Гаусс, Лобачевский постулат Эвклида о параллельных по- прежнему не казался очевидным для разума. Сомнения в его истинности и привели, в конечном счёте, к созданию неевклидовых геометрий. И первопроходцами на этом пути стали, как известно, русский математик Н.И. Лобачевский и венгр Я. Бойяи, которые предложили первые системы неевклидовых геометрий (так называемые параболические геометрии). В этих геометриях пятый постулат гласил, что через точку на плоскости по отношению к данной прямой можно провести более одной параллельной ей прямой. Но это говорило о том, что: а) интуитивная очевидность аксиом научной теории не должна рассматриваться в качестве критерия их истинности; б) интуитивная очевидность не является чем-то обязательным; в) интуитивная очевидность формируется в процессе обучения и является во многом результатом привычки. Более того, как убедительно показал опыт построения различных теорий, различение исходных и производных высказываний теории во многом является делом условным, относительным и конвенциональным. Например, в геометрии Эвклида в качестве пятого постулата можно принять утверждение, что сумма углов любого треугольника равна 2π. В такой системе эвклидовой геометрии утверждение о том, что на плоскости через точку по отношению к данной прямой можно провести более одной прямой, параллельной данной, выводится как теорема [12]. Одним словом, в любой дедуктивно-аксиоматической теории многие аксиомы и теоремы можно менять местами и достигать при этом каждый раз логического замыкания  всех истинных высказываний теории друг на друга. Однако, в целом, при аксиоматическом способе построения теории на роль аксиом стараются выбрать содержательно наиболее простые из всех высказываний теории, а содержательно более сложные вывести из них в качестве логических следствий (теорем).

 В отличие от математики, в логике при решении вопроса об истинности аксиом ее теорий гносеологическая ситуация выглядит намного проще. Дело в том, что в логике критерием истинности ее аксиом является их правильная логическая форма, наличие которой гарантирует их логическую истинность [4; 13]. Например, такие аксиомы исчисления высказываний, к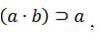ак   являются всегда истинными просто в силу своей логической формы, независимо от истинности или ложности входящих в эти аксиомы элементарных высказываний a и b. Но наиболее сложная ситуация в науке обстоит с доказательством истинности аксиом естественнонаучных и социально-гуманитарных теорий. В рабочем порядке, с точки зрения стандартных когнитивных техник, истинность исходных принципов и аксиом естественнонаучных или социально-гуманитарных теорий обычно принимается условно, на основе конвенции и как бы отпускается им в кредит [7]. Правда, впоследствии аксиомы теории обязаны будут оправдать или «отработать» этот кредит, во-первых,  путем логического развертывания всего содержания теории из ее аксиом, а, во-вторых, путем их практического использования в качестве инструмента систематизации, предсказания и роста научного знания. Но, конечно, это не означает, что процесс введения аксиом в ту или иную теорию является произвольным и ничем не детерминированным актом. Это далеко не так.

Во-первых, кандидаты на роль аксиом той или иной теории выбираются среди уже имеющегося множества высказываний той или иной научной дисциплины, истинность многих из которых была подтверждена ранее эмпирическим путём. Например, при аксиоматическом построении эвклидовой геометрии в Древней Греции, многие проверенные на практике геометрические построения были заимствованы античными математиками из арсенала геометрических знаний древних египтян. Или другой аналогичный пример, но уже из физики. Такие аксиомы классической механики как закон всемирного тяготения, закон инерции и закон о прямо пропорциональной зависимости ускорения тела от величины приложенной силы были известны учёным и имели опытное подтверждение еще до построения механики И. Ньютона [6; 9].

Далее. Самый трудный и творческий момент – выбор некоторых из известных истин в качестве аксиом теории, также не является абсолютно произвольным и никак не регулируемым волевым актом исследователя. Воля исследователя достаточно жестко детерминирована трудной, хотя возможно и достижимой целью: подобрать в качестве аксиом такое небольшое число истинных высказываний, из которых все остальные истинные высказывания теории следовали бы с логической необходимостью. И вообще-то ни откуда не следует, что такая задача в каждом конкретном случае будет иметь положительное решение. Здесь надежда на комбинаторный талант и удачу исследователя. Так, в своих воспоминаниях о поиске аксиом (основных законов) небесной механики И. Кеплер утверждал, что он перепробовал около 70 вариантов основных законов этой теории, и только после этого огромного и во многом рутинного труда удача снизошла до него [6]. Сам И. Кеплер считал, что это было даровано ему Богом, любовь к которому и вера в совершенную мудрость творца при создании природы не покидали его в течение всей жизни. Столь же большую благодарность к Богу выражал И. Ньютон, когда (о чудо!) открытые до создания механики Ньютона законы Кеплера неожиданно появились в качестве логических следствий аксиом механики Ньютона [9].

В-третьих, для полного доказательства того, что некоторые положения теории, выдвинутые в качестве её аксиом, являются действительно необходимым и достаточным основанием некоторой теории, требуется (как об этом убедительно свидетельствует история науки) очень большое время и усилия не одного поколения учёных, работающих в соответствующей области науки. Наиболее яркие свидетельства, доказывающие справедливость данного положения, даёт, например, история математики, где эта проблема и ставится и решается наиболее строго по сравнению с остальными областями научного знания. Рассмотрим в этой связи примеры с эвклидовой геометрией, арифметикой натуральных чисел и теорией вероятности, самыми простыми, и вместе с тем, самыми основополагающими теориями всей математики. Начнём с эвклидовой геометрии. После построения Эвклидом геометрии дедуктивно-аналитическим способом среди математиков долгое время, почти до конца XIX в., царило убеждение, что она является строго (логически) доказательной системой, что её основу составляет пять известных аксиом, что эти аксиомы образуют необходимую и достаточную основу логического выведения из них всех остальных истинных высказываний этой теории. Эта теория на протяжении 20 веков считалась парадигмальной для построения теорий во всех других областях науки. Как известно, И. Ньютон сознательно исходил из такой установки при построении своей теории механического движения, а Б. Спиноза даже при построении этической теории. Даже тогда, когда в 30-е годы XIX в. были построены системы неэвклидовых геометрий, убеждение в необходимости и достаточности (полноты) системы аксиом эвклидовой геометрии не было не только поколеблено, но скорее даже укрепилось. Так из этой веры вытекало убеждение в том, что и система аксиом геометрии Лобачевского, также состоящая из пяти аксиом, хотя и является альтернативной геометрии Эвклида, однако, также является для неэвклидовой геометрии необходимой и достаточной основой доказательства всех её теорем.  Правда, историки математики, да и сам Эвклид, склонны были считать, что число аксиом эвклидовой геометрии больше пяти, так как в это число необходимо включить не только чисто геометрические положения, но и ряд правил вывода, имеющих не геометрическое содержание, а скорее логическое, а также алгебраическое. Таких аксиом в системе Эвклида было девять. Вот некоторые из них: «Если к равным прибавить или отнять равное, то получим равное», «Если все точки фигуры при их наложении (совмещении) совпадают, то эти фигуры равны», «если А=В, а В=С, то А=С», «Если А≠В и А+С=D, то В+С≠D» [8; 11, c. 303–305]. Вторая из упомянутых выше аксиом впоследствии получила название аксиомы движения, а третья является логическим правилом, известным под названием правила подстановки.  Таким образом, полная система аксиом эвклидовой геометрии состояла не из 5 утверждений, как это долгое время утверждали все традиционные учебники геометрии, а минимум из 14 [3]. При этом аксиома движения – это явно геометрическое по содержанию высказывание, поскольку в ней речь идёт о геометрических фигурах. Кстати, если это признать, тогда становится непонятным статус аксиомы Эвклида, утверждающей, что все прямые углы равны, ибо она может быть выведена как одно из следствий аксиомы движения, но тогда надобность в ней как аксиоме отпадает. Аналогичные рассуждения и аргументы в отношении неопределенного числа аксиом можно бы высказать и в адрес неэвклидовых геометрий Лобачевского, Бойаи и Римана.

Однако, строгое доказательство того, что система аксиом Эвклида была заведомо неполной, даже если принять во внимание соответствующие оговорки самого Эвклида и его комментаторов, осуществил Д. Гильберт. И сделано это было лишь в конце XIX в., а именно в 1899 г. [2].

Доказательство Гильберта означало, что геометрия и самого Эвклида, и та, которая излагалась и излагается ещё и сегодня во всех школьных учебниках геометрии, не являются строго доказательными теориями.

При доказательстве многих их теорем неявно (так сказать «контрабандой») используются положения, которые не являются  заявленными аксиомами  и не вытекают из последних в качестве их следствий. А это противоречит самой идее дедуктивно-аксиоматического способа построения знания.  Так, в эвклидовой геометрии никак не было аксиоматически задано содержание таких геометрических свойств и понятий, как «принадлежать», «находиться на», «пересекаться», «быть непрерывными» и др. А ведь все эти понятия использовались при описании геометрических объектов и доказательстве соответствующих утверждений о них. И всему этому было причиной то, что эвклидова геометрия была содержательной системой знания, а всякая содержательная система неминуемо опирается на интуицию, которая в свою очередь опирается на некий пласт неявного, лишь подразумеваемого знания, что в корне противоречит самой идее строго доказательного знания. Во многом такое положение дел было обусловлено тем, что сама геометрия понималась во многом как физика, как наука о реальном, то есть видимом пространстве. Соответственно при доказательстве многих геометрических положений использовались (якобы только для наглядности) чертежи, а вместе с ними неизбежно вводился неопределённый и не фиксируемый пласт неявного знания. Например, при построении с помощью чертежей прямых линий и плоскостей как бы само собой подразумевалось такое их свойство как непрерывность. Но вообще-то ничто не мешает нам представлять линии или плоскости как прерывистые или имеющие дырки. Более того, видимо для таких объектов с определенной повторяемостью или фиксированной структурой дырок может быть построена своя геометрия. Отсюда Гильберт сделал глубокий и решительный для математики вывод. Он состоял в следующем: аксиоматическое построение любой теории возможно только при условии полного отвлечения от содержания её понятий и их жесткой связью с какой-либо конкретной областью их значений. А чтобы достичь этого, существует только один путь: формализация имеющейся содержательной теории, отображение её высказываний на некоторый формальный (символический) язык, одним словом – построение для содержательной теории её формализованной модели. Конечно, в формализованной теории также имеется определённое содержание, но это содержание ограничено только распознаванием символов и строчек символов, способностью их различения и отождествления, а также умением отличать правильно построенные строчки символов как разрешенных в данной формальной системе конструкций от неправильных, незаконных строчек символов. При таком подходе полностью исключается использование конкретной содержательной интуиции при употреблении тех или иных понятий теории, ибо понятия превращаются или отображаются в символы, которые требуют для своей фиксации в качестве объектов лишь их чувственное восприятие. Осуществив формализацию содержательной (но не логичной) части традиционной эвклидовой геометрии Гильберт показал и доказал, что дедуктивно-аксиоматическое логически доказательное построение этой теории требует введения как минимум 20 аксиом, а отнюдь не 5 или даже 14, как думали все геометры до Гильберта. Мы не будем приводить полностью всю систему аксиом эвклидовой геометрии в исполнении Д. Гильберта [2]. Отметим лишь только, что Гильберт ввёл пять групп аксиом. В каждой из групп аксиомы описывают вполне определённые геометрические свойства и отношения между объектами. Так, первая группа из 8 аксиом это аксиомы «принадлежности», вторая группа из 4 аксиом – аксиомы «порядка», третья группа из 5 аксиом описывает отношение «равенства», «конгруэнтности», четвёртая группа состоит только из 1 аксиомы – аксиомы о параллельности, и, наконец, пятая группа из 2 аксиом определяет отношение «непрерывности». Оценивая построенную им систему эвклидовой геометрии, Д. Гильберт подчёркивал, что и она в строгом смысле не является дедуктивно-аксиоматической, так как в ней отсутствует в явном виде перечень и описание правил логического вывода,  только в соответствии с которыми и можно осуществлять переход от аксиом к теоремам, от одних теорем к другим как их следствиям и т.д. Чтобы построить эвклидову геометрию как полностью дедуктивно-аксиоматическую систему, необходимо формализовать не только геометрическую, но и логическую часть этой системы.

Ярким подтверждением этого тезиса являются попытки математиков построить дедуктивно-аксиоматическим методом другую фундаментальную математическую теорию – арифметику натуральных чисел. Примечательно, что,  несмотря на большую простоту арифметики натуральных чисел по сравнению с эвклидовой геометрией, попытки изложения её содержания дедуктивно-аксиоматическим способом были предприняты лишь  в конце XIX в., то есть спустя более двух тысяч лет после дедуктивно-аксиоматической системы геометрии Эвклида.

И одна из первых попыток дедуктивно-аксиоматического построения арифметики была предпринята также Д. Гильбертом [2]. По аналогии с аксиоматическим построением эвклидовой геометрии Д. Гильберт также разбивает в целях лучшего обозрения и простоты  все введённые им аксиомы на группы. Он выделяет четыре группы аксиом арифметики. Это: 1) аксиомы соединения (6 аксиом); 2) вычислительные аксиомы (6 аксиом); 3) аксиомы порядка (4 аксиомы); 4) аксиома непрерывности. Вот эти аксиомы.

I. Аксиомы соединения.

I_1. Из числа a и числа b при помощи «сложения» получается вполне определённое число c, что обозначается так:

a+b=с  или  b+a=c.

I_2. Для любых двух чисел a и b существует одно и только одно число х, для которого:

a+x=b,

а также одно и только одно число y, для которого:

y+a=b.

I_3. Существует некоторое вполне определённое число – его называют 0 – такое, что для любого а, как:

a+0=а,

так и:

0+a=а.

I_4. Из числа a и числа b получается некоторым другим способом, посредством «умножения», некоторое определённое число с, что обозначается так:

ab=с  или  с=аb.

I_5. Для любых двух чисел a и b, причем число а не 0, существует одно и только одно число х, для которого:

ax=b,

и одно и только одно число y, для которого:

ya=b.

I_6. Существует некоторое вполне определённое число – его называют 1 – такое, что для любого а, как:

a·1=а,

так и:

1·a=а.

II.  Вычислительные аксиомы.

Для любых чисел a, b, c имеют место следующие равенства:

II_1. a+(b+c)=(a+b)+c (ассоциативный закон сложения),

II_2. a+b=b+a (коммутативный закон сложения),

II_3.  a(bc)=(ab)c (ассоциативный закон умножения),

II_4.a(b+c)=ab+ac (дистрибутивность сложения относительно умножения слева),

II_5.(a+b)c=ac+ab (дистрибутивность сложения относительно умножения справа),

II_6. ab=ba (коммутативный закон умножения).

III. Аксиомы порядка

III_1. Из любых двух отличных друг от друга чисел a и b всегда одно определенное число (например, a) больше (>) другого; про это последнее говорят, что оно меньше первого. Это обозначается так:

а>b или b<a.

Ни для какого числа а не может иметь место соотношение а>а.

III_2. Если a>b и b>с, то a>с.

III_3.  Если a>b, то:

 a+c>b+c  и c+а>c+b.

III_4. Если a>b и с>0, то:

 aс>bс и  са>сb.

IV. Аксиомы непрерывности

IV_1. (Аксиома Архимеда). Пусть,  а>0 и b>0 – любые два числа; в таком случае всегда можно число a повторить слагаемым столь большое число раз, чтобы образовавшаяся в результате сумма обладала следующим свойством:

a+а+а+…+а>b.

IV_2.(Аксиома полноты). К системе чисел невозможно присоединить никакой другой системы вещей так, чтобы в системе, образовавшейся в результате этого присоединения, при сохранении прежних соотношений между числами выполнялись бы все аксиомы I, II, III, IV₁. Короче, числа образуют такую систему вещей, которая при сохранении всех взаимоотношений и всех указанных выше аксиом, не поддаётся никакому расширению.

Таким образом, система аксиом арифметики Гильберта включает 17 аксиом. Хотя предложенная Д. Гильбертом система аксиом арифметики оказалась полной, однако, вместе с тем, избыточной. И на это обращал внимание сам Гильберт, так как некоторые из 17 аксиом могли быть получены в качестве следствий из других аксиом системы, то есть не являлись независимыми.

Например, аксиома I₃ есть следствие аксиом I₁, I₂ и II₁, а

аксиома I₆ есть следствие аксиом I₄, I₅ и II₃,

аксиома II₂ – следствие аксиом I₄, II₁, II₄, II₅,

аксиома II₆ – следствие аксиом I, II_1-5, III, IV₁ [8, c. 317–319].

Первоначально эта система арифметики имела своим основанием следующие четыре аксиомы:

1.      Нуль есть число.

2.      Если а – число, то a' также является числом.   

3.      Из a'= b' следует a= b.

4.      Для всякого а, a'=0.

Здесь символ a' означает «непосредственно следующий за а».

     Однако позже было показано, что эта система аксиом не является полной для арифметики натуральных чисел, так как в ней не дано определение равенства чисел. Оказалось, что для определения равенства чисел необходимо ввести ещё четыре аксиомы:

5.      а+0=а.

6.      а+u'= (а+u)'.

7.      a·0=0.

8.      а·u'= (а·u)+a.

Но и эта система из 8 аксиом оказалась не полной. Необходимо было также ввести аксиому математической индукции, с помощью которой можно было бы доказывать универсальные суждения о некоторых свойствах чисел.

Аксиома индукции имеет следующий вид: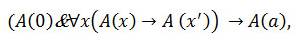где её символы обозначают следующее:

А – некоторое свойство натурального числа (например, «быть чётным числом», «быть  нечётным числом», «быть простым числом» и т.д.),

0 – ноль,

' – следующий за,

А – любое (всякое) натуральное число,

→ знак логического следования.

Таким образом, оказалось, что полная система аксиом арифметики натуральных чисел (без правил логики) должна состоять как минимум из девяти аксиом [8].

Еще позже были построены дедуктивно-аксиоматическим способом другие математические теории. Так, только в 30-х годах XX в.  удалось построить  этим методом такую математическую дисциплину, как теория вероятностей – основу математической статистики и всех статистических конкретно-научных теорий от термодинамики до квантовой механики, биологии,  генетики, лингвистики, социологии и других  научных теорий, пришедших в XX в. на смену классическим детерминистским теориям. Большую подготовительную работу для осуществления решающего шага в аксиоматическом построении теории вероятностей осуществили Дж. Гиббс,  Г. Рейхенбах, Э. Борель, М. Смолуховский, русский и советский математик С.Н. Бернштейн. Но только выдающемуся  отечественному математику А.Н. Колмогорову удалось завершить их работу и поставить в 30-х годах победную точку в решении этой проблемы. Но главным основанием здесь явилось формально-аксиоматическое  определение вероятности как некоторой специфической математической функции, свойства которой задаются небольшим списком аксиом. С помощью этих аксиом давалось лишь неявное определение вероятности, благодаря чему она отделялась от ее возможных  интерпретаций, обусловленных разными сферами ее применения [5] .

В построенной А.Н. Колмогоровым аксиоматической теории вероятности сначала вводится понятие (математический конструкт) «множество (пространство) случайных событий». Под случайными событиями понимаются такие, которые могут произойти, а могут и не произойти. Вероятность это действительное число в интервале {0,1}, которое является значением меры, а именно степени возможности некоторого случайного события при определенных условиях. Формально вероятность p понималась как математическая функция, подчиняющаяся следующим аксиомам:

1. 0≤ p(А)≤1.

2. p(A+B)=p(A)+p(B), где A и B – независимые друг от друга случайные события.

      3. p(A+A)=1 (вероятность необходимого события).

4. p(A·A)=0 (вероятность невозможного события) [15].

        Таким образом, при формально-аксиоматическом построении теории вероятностей вероятность не определяется явным образом. Точно также как не определялись явным образом понятия «точки», «прямой» и плоскости в формально-аксиоматической системе эвклидовой геометрии Д. Гильберта. С точки же зрения применимости аксиоматической теории вероятностей  под «вероятностью» можно и должно понимать любое реальное отношение, свойства которого отвечают аксиомам исчисления вероятности. Как оказалось, это может быть не только «относительная частота» некоторых событий по отношению к другому классу событий, но и «степень объективной возможности» реализации некоторого свойства при определенных условиях, и «степень подтверждения» одного высказывания (гипотезы) другими высказываниями (данными), и «степень уверенности» субъекта в истинность некоторой гипотезы или в наступление некоторого события. Благодаря аксиоматическому определению вероятности удалось примирить различные альтернативные понимания вероятности и показать, что они отнюдь не исключают, а лишь дополняют друг друга, будучи одинаково законными интерпретациями и способами  применения аксиоматически определённого понятия вероятности [6]. Таким образом, при аксиоматическом построении теории появляется возможность не противопоставлять, а примирять различные традиции в истолковании тех или иных понятий и категорий науки. Познавательная деятельность, направленная  на синтез научного знания, оказывается одной из важных гносеологических особенностей и функций теорий, построенных дедуктивно-аксиоматическим методом. Разумеется, при той существенной оговорке, что любой синтез никогда не может быть ни полным, ни окончательным в пределах одной теории. По аналогии с оптическим прибором, любая теория всегда имеет свои определенные возможности и одновременно свой предел «гносеологического разрешения», свои границы и интервал адекватности получаемого отображения действительности. Правда и здесь имеется одно приятное для человеческой гордыни исключение. И этим исключением являются математическая логика и две её фундаментальные теории – исчисление высказываний и исчисление предикатов первого порядка (терминов, обозначающих только свойства предметов, но не их отношения, так называемых «одноместных предикатов»). В отношении этих аксиоматически построенных логических теорий в 30-х и 40-х годах XX в. были строго доказаны: а) их абсолютная полнота и б) их (синтаксическая) непротиворечивость [14; 35]. Правда, столь же строго была доказана принципиальная неполнота и  неразрешимость более сложных теорий математической логики, имеющих дело с двухместными или более местными предикатами, а также с предикатами, обозначающими различного рода модальности (возможно, вероятно, должно, временно, случайно, необходимо и др.). Но всё же фундаментальное основание формальной логики как науки о выводе оказалось ненадёжным в абсолютном смысле этого слова [4].

Таким образом, дедуктивно-аксиоматический способ построения научных теорий используется в основном в математике и логике. И это видимо имеет свою причину. Такой причиной является, на наш взгляд то, что математическое и логическое знание является имманентным продуктом мышления, артефактическим продуктом его конструктивной деятельности, а потому имеющим в своей массе характер аналитических истин, за исключением относительно небольшого числа математических высказываний, выступающих в роли аксиом математических теорий [14]. Истории науки известен лишь один серьёзный прецедент построения научной теории дедуктивно-аксиоматическим способом вне математики  и логики.  И это – классическая механика – И. Ньютона [27]. Конечно, при этом речь не идёт о всей классической механике, опирающейся во всех своих многочисленных теоретических построениях (гидродинамика, термодинамика, теория колебаний, сопротивление материалов, аэродинамика, инженерная теоретическая механика и др.) на механику Ньютона и её аксиомы. Как показал В.С. Стёпин [10], в отношении некоторых разделов классической механики, названных выше, они не могут быть рассмотрены как дедуктивные (логические) следствия механики Ньютона, так как вводят по отношению к последней новое содержание. Но сама классическая механика Ньютона с её тремя законами движения и взаимодействия материальных точек в эвклидовом пространстве, безусловно, является дедуктивно-аксиоматической системой. Полная ли эта система аксиом, представленная законами и принципами механики Ньютона, это уже другой вопрос. Сегодня осознание неполноты механики Ньютона уже никого не может напугать с практической или философской точек зрения, когда мы узнали, что даже геометрия Эвклида, как показал Гильберт, была довольно далека от идеала полноты и чисто логической доказательности. Всё дело лишь в намерениях и достижении определённых положительных результатов на избранном пути.

1. Veyl' G. Matematicheskoe myshlenie. M., 1989.

2. Gil'bert D. Osnovaniya geometrii. M.L. , 1948.

3. Kagan V.F. Ocherki po geometrii. M., 1963.

4. Karri H. Osnovaniya matematicheskoy logiki. M., 1969.

5. Kolmogorov A.N. Osnovnye ponyatiya teorii veroyatnosti. 2-e izd. M., 1974.

6. Lebedev S.A. , Lebedev K.S. Suschestvuet li universal'nyy nauchnyy metod?// Vestnik Tverskogo gosudarstvennogo universiteta. Seriya: filosofiya. 2015. - №2. - S. 56-72.

7. Lebedev S.A. Metody nauchnogo poznaniya. M.: Al'fa-M. 2014. - 272 s.

8. Nachala Evklida. Per. s grech. D.D. Morduhay-Boltovskogo. Knigi I-VI. M.-L., 1948.

9. N'yuton I. Matematicheskie nachala natural'noy filosofii. M., 1989.

10. Stepin V.S. Teoreticheskoe znanie. M. 2000.

11. Uspenskiy V.A. Apologiya matematiki. SPb, 2009.

12. Filosofiya matematiki i tehnicheskih nauk. Pod obschey red. S.A. Lebedeva. M.: Akademicheskiy proekt. 2006. - 779 s.

13. Cherch A. Vvedenie v matematicheskuyu logiku. M., 2012.

14. Lebedev S.A. Principles of mathematic theories// Voprosy filosofii i psihologii. 2015. №2(4). S. 100-111.

15. Lebedev S.A. Axiomatic and genetic-construction methods of theoretical cognition: comparative analysis//European Journal of Philosophical Research. 2015. № 2(4). C. 72-82.