Moskva, Moscow, Russian Federation
Moskva, Moscow, Russian Federation
Graphic discipline at all times causing serious difficulties for most students, and now does no longer available to them. In these circumstances, it is necessary to determine the place of descriptive geometry in higher technical education. Descriptive geometry is only a means of information transmission. in this discipline in the university course involves teaching students the basic rules of constructions, certain techniques and methods. But the main stage - direct work with stereometric objects - students in higher education is not currently practiced. This situation raises doubts about the necessity of studying descriptive geometry, while the development of graphical software package bears the clear benefit of future specialists. It is obvious that certain rules of construction laid down in the graphic editors, and the one who was the program understands how to construct the tangent to the ellipse, and the ellipse itself. A user is working with a model of the space, which, like all models has an error in comparison with the original. This geometry can hardly make even small opening. Based on the above, we can conclude that it is necessary to support the methods and techniques of descriptive geometry, studying them in depth with talented students, to keep so domestic science. Otherwise, we risk permanently stay only foreign research users.
descriptive geometry, geometry, spatial reasoning, the tangent to the ellipse, the properties of the ellipse, graphics editor.
Начертательная геометрия – графическая дисциплина, которую изучают студенты технических и других вузов. В нашей стране впервые курс начертательной геометрии прочитан в 1810 г. в Петербургском институте корпуса инженеров путей и сообщения французским инженером К.И. Потье. С того времени ситуация в области передовых технологий изменилась. Особенно сейчас, в связи с широким распространением компьютерных технологий, начертательная геометрия и многие другие технические дисциплины кажутся ненужными, так как компьютерные программы совершают сложнейшие действия вместо человека. Ситуация в настоящее время усугублена еще и демографической катастрофой, которая не позволяет вузам обеспечить конкурс, как следствие – необходимый уровень подготовки первокурсников. Графические дисциплины во все времена вызывали серьезные трудности у большинства студентов, а теперь и вовсе становится недоступным для них. В журнале «Геометрия и графика» уделяется внимание роли начертательной геометрии в современном техническом образовании [4–8].
В сложившихся обстоятельствах необходимо определить место начертательной геометрии в высшем техническом образовании.
При рассмотрении данного вопроса надо учитывать разницу между инженером и ученым. Инженер-практик обязан уметь пользоваться современными техническими средствами и быстро реагировать на их постоянное совершенствование. Ученый-теоретик должен понимать суть вещей, которая со времен Эвклида остается неизменной.
Начнем с определения. Начертательная геометрия – графический язык, с помощью которого передается информация о n-мерном пространстве путем проецирования его на m-мерное пространство (m = 2–n) [3]. Иными словами, начертательная геометрия – лишь средство передачи информации. Как известно, любое знание развивается только при наличии терминологического аппарата, с помощью которого люди имеют возможность выражать свои мысли. Курс по этой дисциплине в вузе подразумевает обучение студентов основным правилам построений, некоторым приемам и методам. Но основной этап – непосредственная работа со стереометрическими объектами – студентами – в вузе в настоящее время не практикуется. Такое положение вещей вызывает сомнение в надобности изучения начертательной геометрии, в то время как освоение графического программного пакета несет явную пользу будущему специалисту. Отметим, что работа с программой реализуется при изготовлении цифровых трехмерных моделей и чертежей. Мысленная работа с пространством и дальнейшим построением проекций наилучшим образом реализуется при решении задач по начертательной геометрии.
В решениях таких задач можно выделить два основных этапа:
- стереометрическое решение задачи, т.е. мысленное моделирование пространственных объектов на основе законов стереометрии;
- изложение сути решения на бумаге с помощью начертательной геометрии.
Эти этапы не обязательно строго следуют друг за другом и являются, скорее, типами умственной деятельности, реализуемой в процессе решения.
Надо отметить, что второй этап выполнения осуществим средствами компьютерного моделирования. Однако существует значительная разница между представленными двумя способами реализации второго этапа.
Понять эту разницу помогут следующие простые примеры.
Дана задача: Найти касательную прямую m к сфере, в заданной точке А, принадлежащей этой сфере (решать в одной проекции).
Вначале необходимо в уме понять, что искомая касательная является также касательной к плоскому сечению сферы, проходящему через ее центр (экваториальная окружность, проходящая через заданную точку). Это этап мысленного стереометрического решения. После необходимо выразить свою мысль либо при помощи начертательной геометрии, либо средствами программного обеспечения. Например, в программе «КОМПАС» 2D решение такой задачи выглядит следующим образом (см. рис. 1).

Строим эллипс (проекцию экваториального сечения) по заданным центру и трем точкам с помощью специальной функции. Затем, применив функцию «касательная в точке», строим искомую прямую.
Такое решение отнимает мало времени, оно наглядно и понятно каждому образованному человеку, даже далекому от технических специальностей.
Теперь рассмотрим решение этой задачи средствами начертательной геометрии (см. рис. 2а, б).

Внизу слева приведена зависимость положения точки, принадлежащей эллипсу, от величины большой и малой осей [1, 2]. Пользуясь этой зависимостью, находим величину малой оси эллипса, который является проекцией окружности, проходящей через точку А и принадлежащей сфере (рис. 2а).
Сам эллипс мы не строим, так как в решении эта линия не участвует. Далее находим фокусы этого эллипса в соответствии с правилом r = OS (см. рис. 2). Мы знаем, что биссектриса m угла между FA и F’A есть касательная к эллипсу [1, 2].
Отметим, что для такого решения необходимо знать три справочных (стандартных) способа: способ построения эллипса, прием нахождения фокусов эллипса, способ нахождения касательной к эллипсу в заданной точке. Поэтому в целом такое решение выглядит громоздко и сложно для понимания.
Такая задача часто является одним из этапов в более сложных комплексных решениях. Когда студент сталкивается с таким заданием, но не знает всех описанных выше способов, он пытается найти свой собственный. Интересно, что многие из ребят самостоятельно приходят к открытию альтернативного способа, который, как ни странно, не описан в известных нам учебниках.
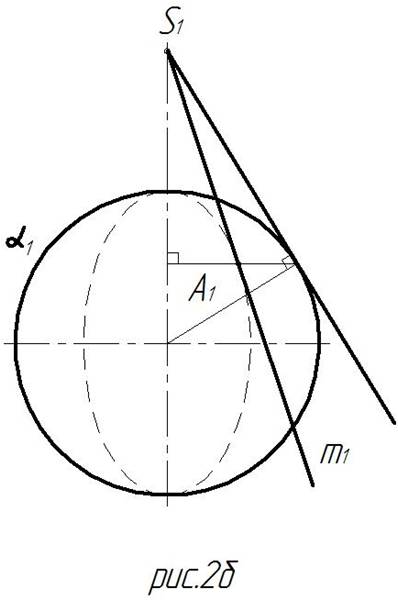
Альтернативный способ показан на рис. 2б. Эллипс начерчен для наглядности и в решении не участвует. В основе метода лежит следующее рассуждение: касательные к сфере, пересекающие ее параллель, сходятся в одной точке и образуют коническую поверхность. Поэтому, построив касательную к очерку сферы и найдя вершину конуса S, можно провести искомую прямую. Отметим, что, кроме решения поставленной задачи, мы еще и открыли новый способ построения касательной к эллипсу, который, вероятно, окажется более удобным в некоторых случаях.
Такие мини-открытия часто делают участники олимпиад по начертательной геометрии, подчас поражая даже авторов задач своей находчивостью.
Очевидно, что в графических редакторах заложены некие правила построения, и тот, кто составлял программу, прекрасно понимал, каким образом строится касательная к эллипсу, а также сам эллипс. А пользователь работает с моделью пространства, которая, как и все модели, имеет погрешность в сравнении с оригиналом. Такой геометр едва ли совершит хотя бы мини-открытие.
Напротив, начертательная геометрия выводит нас на непосредственное оперирование идеальными объектами – окружность, прямая, точка (три функции, которыми имеет право пользоваться геометр).
Исходя из изложенного, можно сделать вывод: необходимо поддерживать методы и приемы начертательной геометрии, углубленно изучая их со способными студентами, и, таким образом, сохранять отечественную науку. В противном случае мы рискуем навсегда остаться только пользователями чужих разработок.
1. Sal´kov, N.A. EHllips: kasatel´naya i normal´ [Text] / N.A. Sal´kov // Geometriya i grafika. - 2013. - T. 1. - №1. - Рр. 35-37.
2. Bermant, A.F. Graficheskij spravochnik po matematike atlas krivyh [Text] / A.F. Bermant. - Moskva, Leningrad: Ob"edinennoe nauchno-tekhnicheskoe izdatel´stvo NKTP SSSR, 1937. - 211 р.
3. Sal´kov, N.A. Nachertatel´naya geometriya: bazovyj kurs: uchebnoe posobie [Text] / N.A. Sal´kov. - M: INFRA-M, 2013. - 184 р.
4. Stolbova, I.D. Aktual´nye problemy graficheskoj podgotovki studentov tekhnicheskih vuzov [Text] / I.D. Stolbova // Geometriya i grafika. - 2014. - T. 2. - № 1. - Рр. 30-41. -DOI:https://doi.org/10.12737/3846.
5. Vol´hin, K.A. Problemy graficheskoj podgotovki studentov tekhnicheskogo universiteta [Text] / K.A. Vol´hin T.A. Astahova // Geometriya i grafika. - 2014. - T. 2. - № 3. - Рр. 25-30. -DOI:https://doi.org/10.12737/6522.
6. Vyshnepol´skij, V.I. Celi i metody obucheniya graficheskim disciplinam [Text] / V.I. Vyshnepol´skij, N.A. Sal´kov // Geometriya i grafika. - 2013. - T. 1. - № 2. - Р. 8, 9. -DOI:https://doi.org/10.12737/777.
7. Ivanov, G.S. Perspektivy nachertatel´noj geometrii, kak uchebnoj discipliny [Text] / G.S. Ivanov // Geometriya i grafika. - 2013. - T. 1. - № 1. - Р. 26, 27. - DOI:https://doi.org/10.12737/467.
8. Tihonov-Bugrov, D.E. O nekotoryh problemah graficheskoj podgotovki v tekhnicheskih vuzah [Text] / D.E. Tihonov-Bugrov // Geometriya i grafika. - 2014. - T. 2. - № 1. - Рр. 46-52. - DOI:https://doi.org/10.12737/3848.






